Implementing a JIT Compiled Language with Haskell and LLVM
Adapted by Stephen Diehl ( @smdiehl )
This is an open source project hosted on Github. Corrections and feedback always welcome.
The written text licensed under the LLVM License and is adapted from the original LLVM documentation. The new Haskell source is released under the MIT license.
Chapter 1 ( Introduction )
Welcome to the Haskell version of "Implementing a language with LLVM" tutorial. This tutorial runs through the implementation of a simple language, and the basics of how to build a compiler in Haskell, showing how fun and easy it can be. This tutorial will get you up and started as well as help to build a framework you can extend to other languages. The code in this tutorial can also be used as a playground to hack on other LLVM specific things. This tutorial is the Haskell port of the C++, Python and OCaml Kaleidoscope tutorials. Although most of the original meaning of the tutorial is preserved, most of the text has been rewritten to incorporate Haskell.
An intermediate knowledge of Haskell is required. We will make heavy use of monads and transformers without pause for exposition. If you are not familiar with monads, applicatives and transformers then it is best to learn these topics before proceeding. Conversely if you are an advanced Haskeller you may notice the lack of modern techniques which could drastically simplify our code. Instead we will shy away from advanced patterns since the purpose is to instruct in LLVM and not Haskell programming. Whenever possible we will avoid cleverness and just do the "stupid thing".
The overall goal of this tutorial is to progressively unveil our language, describing how it is built up over time. This will let us cover a fairly broad range of language design and LLVM-specific usage issues, showing and explaining the code for it all along the way, without overwhelming you with tons of details up front.
It is useful to point out ahead of time that this tutorial is really about teaching compiler techniques and LLVM specifically, not about teaching modern and sane software engineering principles. In practice, this means that we'll take a number of shortcuts to simplify the exposition. If you dig in and use the code as a basis for future projects, fixing these deficiencies shouldn't be hard.
I've tried to put this tutorial together in a way that makes chapters easy to skip over if you are already familiar with or are uninterested in the various pieces. The structure of the tutorial is:
Chapter #1: Introduction to the Kaleidoscope language, and the definition of its Lexer - This shows where we are going and the basic functionality that we want it to do. LLVM obviously works just fine with such tools, feel free to use one if you prefer.
Chapter #2: Implementing a Parser and AST - With the lexer in place, we can talk about parsing techniques and basic AST construction. This tutorial describes recursive descent parsing and operator precedence parsing. Nothing in Chapters 1 or 2 is LLVM-specific, the code doesn't even link in LLVM at this point. :)
Chapter #3: Code generation to LLVM IR - With the AST ready, we can show off how easy generation of LLVM IR really is.
Chapter #4: Adding JIT and Optimizer Support - Because a lot of people are interested in using LLVM as a JIT, we'll dive right into it and show you the 3 lines it takes to add JIT support. LLVM is also useful in many other ways, but this is one simple and "sexy" way to show off its power. :)
Chapter #5: Extending the Language: Control Flow - With the language up and running, we show how to extend it with control flow operations (if/then/else and a ‘for' loop). This gives us a chance to talk about simple SSA construction and control flow.
Chapter #6: Extending the Language: User-defined Operators - This is a silly but fun chapter that talks about extending the language to let the user program define their own arbitrary unary and binary operators (with assignable precedence!). This lets us build a significant piece of the "language" as library routines.
Chapter #7: Extending the Language: Mutable Variables - This chapter talks about adding user-defined local variables along with an assignment operator. The interesting part about this is how easy and trivial it is to construct SSA form in LLVM: no, LLVM does not require your front-end to construct SSA form!
Chapter #8: Conclusion and other useful LLVM tidbits - This chapter wraps up the series by talking about potential ways to extend the language.
This tutorial will be illustrated with a toy language that we'll call Kaleidoscope (derived from "meaning beautiful, form, and view" or "observer of beautiful forms"). Kaleidoscope is a procedural language that allows you to define functions, use conditionals, math, etc. Over the course of the tutorial, we'll extend Kaleidoscope to support the if/then/else construct, a for loop, user defined operators, JIT compilation with a simple command line interface, etc.
Setup
You will need either GHC 7.8 or GHC 7.10.
You will of course also need LLVM 3.3 or 3.4 (not 3.2 or earlier) installed on your system. Run the command for your Linux distribution:
$ pacman -S llvm # Arch Linux
$ apt-get install llvm # Debian/Ubuntu
$ emerge llvm # Gentoo
$ yum install llvm # SuSE LinuxThe included "kaleidoscope.cabal" will install the necessary Haskell bindings. It is recommended that you work within a sandbox:
$ cabal sandbox init
$ cabal configure
$ cabal install --only-dependenciesAlternatively the Nix package manager ( or NixOS ) can be used to provision the entire environment including llvm, llvm-general and ghc.
$ nix shellThe Basic Language
Because we want to keep things simple, the only datatype in Kaleidoscope is a 64-bit floating point type (aka ‘double' in C parlance). As such, all values are implicitly double precision and the language doesn't require type declarations. This gives the language a very nice and simple syntax. For example, the following simple example computes Fibonacci numbers:
# Compute the x'th fibonacci number.
def fib(x)
if x < 3 then
1
else
fib(x-1)+fib(x-2)
# This expression will compute the 40th number.
fib(40)We also allow Kaleidoscope to call into standard library functions (the LLVM JIT makes this completely trivial). This means that we can use the ‘extern' keyword to define a function before we use it (this is also useful for mutually recursive functions). For example:
extern sin(arg);
extern cos(arg);
extern atan2(arg1 arg2);
atan2(sin(.4), cos(42))A more interesting example is included in Chapter 6 where we write a little Kaleidoscope application that displays a Mandelbrot Set at various levels of magnification.
Lets dive into the implementation of this language!
LLVM Introduction
A typical compiler pipeline will consist of several stages. The middle phase will often consist of several representations of the code to be generated known as intermediate representations.

LLVM is a statically typed intermediate representation and an associated toolchain for manipulating, optimizing and converting this intermediate form into native code. LLVM code comes in two flavors, a binary bitcode format (.bc) and assembly (.ll). The command line tools llvm-dis and llvm-as can be used to convert between the two forms. We'll mostly be working with the human readable LLVM assembly and will just refer to it casually as IR and reserve the word assembly to mean the native assembly that is the result of compilation. An important note is that the binary format for LLVM bitcode starts with the magic two byte sequence ( 0x42 0x43 ) or "BC".
An LLVM module consists of a sequence of toplevel mutually scoped definitions of functions, globals, type declarations, and external declarations.
Symbols used in an LLVM module are either global or local. Global symbols begin with @ and local symbols begin with %. All symbols must be defined or forward declared.
declare i32 @putchar(i32)
define i32 @add(i32 %a, i32 %b) {
%1 = add i32 %a, %b
ret i32 %1
}
define void @main() {
%1 = call i32 @add(i32 0, i32 97)
call i32 @putchar(i32 %1)
ret void
}A LLVM function consists of a sequence of basic blocks containing a sequence of instructions and assignment to local values. During compilation basic blocks will roughly correspond to labels in the native assembly output.
define double @main(double %x) {
entry:
%0 = alloca double
br body
body:
store double %x, double* %0
%1 = load double* %0
%2 = fadd double %1, 1.000000e+00
ret double %2
}First class types in LLVM align very closely with machine types. Alignment and platform specific sizes are detached from the type specification in the data layout for a module.
| Type | |
|---|---|
i1 |
A unsigned 1 bit integer |
i32 |
A unsigned 32 bit integer |
i32* |
A pointer to a 32 bit integer |
i32** |
A pointer to a pointer to a 32 bit integer |
double |
A 64-bit floating point value |
float (i32) |
A function taking a i32 and returning a 32-bit floating point float |
<4 x i32> |
A width 4 vector of 32-bit integer values. |
{i32, double} |
A struct of a 32-bit integer and a double. |
<{i8*, i32}> |
A packed structure of a integer pointer and 32-bit integer. |
[4 x i32] |
An array of four i32 values. |
While LLVM is normally generated procedurally we can also write it by hand. For example consider the following minimal LLVM IR example.
declare i32 @putchar(i32)
define void @main() {
call i32 @putchar(i32 42)
ret void
}This will compile (using llc) into the following platform specific assembly. For example march=x86-64 on a Linux system we generate output like following:
.file "minimal.ll"
.text
.globl main
.align 16, 0x90
.type main,@function
main:
movl $42, %edi
jmp putchar
.Ltmp0:
.size main, .Ltmp0-main
.section ".note.GNU-stack","",@progbitsWhat makes LLVM so compelling is it lets us write our assembly-like IR as if we had an infinite number of CPU registers and abstracts away the register allocation and instruction selection. LLVM IR also has the advantage of being mostly platform independent and retargatable, although there are some details about calling conventions, vectors, and pointer sizes which make it not entirely independent.
As an integral part of Clang, LLVM is very well suited for compiling C-like languages, but it is nonetheless a very adequate toolchain for compiling both imperative and functional languages. Some notable languages using LLVM include:
GHC has a LLVM compilation path that is enabled with the -fllvm flag. The library ghc-core can be used to view the IR compilation artifacts.
Full Source
See src/chapter1 for the full source from this chapter.
Chapter 2 (Parser and AST)
Parser Combinators
For parsing in Haskell it is quite common to use a family of libraries known as Parser Combinators which let us write code to generate parsers which itself looks very similar to the BNF ( Backus–Naur Form ) of the parser grammar itself!
Structurally a parser combinator is a collection of higher-order functions which composes with other parsing functions as input and returns a new parser as its output. Our lexer will consist of functions which operate directly on matching string inputs and are composed with a variety of common combinators yielding the full parser. The Parsec library exposes a collection of combinators:
| Combinators | |
|---|---|
<|> |
The choice operator tries to parse the first argument before proceeding to the second. Can be chained sequentially to a generate a sequence of options. |
many |
Consumes an arbitrary number of patterns matching the given pattern and returns them as a list. |
many1 |
Like many but requires at least one match. |
optional |
Optionally parses a given pattern returning it's value as a Maybe. |
try |
Backtracking operator will let us parse ambiguous matching expressions and restart with a different pattern. |
The Lexer
Our initial language has very simple lexical syntax.
integer: 1, -2, 42
integer :: Parser Integer
integer = Tok.integer lexerfloat: 3.14, 2.71, 0.0
float :: Parser Double
float = Tok.float lexeridentifier: a, b, foo, ncc1701d
identifier :: Parser String
identifier = Tok.identifier lexerAnd several tokens which enclose other token(s) returning a compose expression.
parens :: Parser a -> Parser a
parens = Tok.parens lexer
semiSep :: Parser a -> Parser [a]
semiSep = Tok.semiSep lexer
commaSep :: Parser a -> Parser [a]
commaSep = Tok.commaSep lexerLastly our lexer requires that several tokens be reserved and not used identifiers, we reference these as separately.
reserved: def, extern
reservedOp: +, *, -, ;
reserved :: String -> Parser ()
reserved = Tok.reserved lexerreservedOp :: String -> Parser ()
reservedOp = Tok.reservedOp lexerPutting it all together we have our Lexer.hs module.
module Lexer where
import Text.Parsec.String (Parser)
import Text.Parsec.Language (emptyDef)
import qualified Text.Parsec.Token as Tok
lexer :: Tok.TokenParser ()
lexer = Tok.makeTokenParser style
where
ops = ["+","*","-",";"]
names = ["def","extern"]
style = emptyDef {
Tok.commentLine = "#"
, Tok.reservedOpNames = ops
, Tok.reservedNames = names
}
integer :: Parser Integer
integer = Tok.integer lexer
float :: Parser Double
float = Tok.float lexer
parens :: Parser a -> Parser a
parens = Tok.parens lexer
commaSep :: Parser a -> Parser [a]
commaSep = Tok.commaSep lexer
semiSep :: Parser a -> Parser [a]
semiSep = Tok.semiSep lexer
identifier :: Parser String
identifier = Tok.identifier lexer
reserved :: String -> Parser ()
reserved = Tok.reserved lexer
reservedOp :: String -> Parser ()
reservedOp = Tok.reservedOp lexerThe Parser
The AST for a program captures its behavior in such a way that it is easy for later stages of the compiler (e.g. code generation) to interpret. We basically want one object for each construct in the language, and the AST should closely model the language. In Kaleidoscope, we have expressions, and a function object. When parsing with Parsec we will unpack tokens straight into our AST which we define as the Expr algebraic data type:
module Syntax where
type Name = String
data Expr
= Float Double
| BinOp Op Expr Expr
| Var String
| Call Name [Expr]
| Function Name [Expr] Expr
| Extern Name [Expr]
deriving (Eq, Ord, Show)
data Op
= Plus
| Minus
| Times
| Divide
deriving (Eq, Ord, Show)This is all (intentionally) rather straight-forward: variables capture the variable name, binary operators capture their operation (e.g. Plus, Minus, ...), and calls capture a function name as well as a list of any argument expressions.
We create Parsec parser which will scan a input source and unpack it into our Expr type. The code composes within the Parser to generate the resulting parser which is then executed using the parse function.
module Parser where
import Text.Parsec
import Text.Parsec.String (Parser)
import qualified Text.Parsec.Expr as Ex
import qualified Text.Parsec.Token as Tok
import Lexer
import Syntax
binary s f assoc = Ex.Infix (reservedOp s >> return (BinOp f)) assoc
table = [[binary "*" Times Ex.AssocLeft,
binary "/" Divide Ex.AssocLeft]
,[binary "+" Plus Ex.AssocLeft,
binary "-" Minus Ex.AssocLeft]]
int :: Parser Expr
int = do
n <- integer
return $ Float (fromInteger n)
floating :: Parser Expr
floating = do
n <- float
return $ Float n
expr :: Parser Expr
expr = Ex.buildExpressionParser table factor
variable :: Parser Expr
variable = do
var <- identifier
return $ Var var
function :: Parser Expr
function = do
reserved "def"
name <- identifier
args <- parens $ many variable
body <- expr
return $ Function name args body
extern :: Parser Expr
extern = do
reserved "extern"
name <- identifier
args <- parens $ many variable
return $ Extern name args
call :: Parser Expr
call = do
name <- identifier
args <- parens $ commaSep expr
return $ Call name args
factor :: Parser Expr
factor = try floating
<|> try int
<|> try extern
<|> try function
<|> try call
<|> variable
<|> parens expr
defn :: Parser Expr
defn = try extern
<|> try function
<|> expr
contents :: Parser a -> Parser a
contents p = do
Tok.whiteSpace lexer
r <- p
eof
return r
toplevel :: Parser [Expr]
toplevel = many $ do
def <- defn
reservedOp ";"
return def
parseExpr :: String -> Either ParseError Expr
parseExpr s = parse (contents expr) "<stdin>" s
parseToplevel :: String -> Either ParseError [Expr]
parseToplevel s = parse (contents toplevel) "<stdin>" sThe REPL
The driver for this simply invokes all of the compiler in a loop feeding the resulting artifacts to the next iteration. We will use the haskeline library to give us readline interactions for the small REPL.
module Main where
import Parser
import Control.Monad.Trans
import System.Console.Haskeline
process :: String -> IO ()
process line = do
let res = parseToplevel line
case res of
Left err -> print err
Right ex -> mapM_ print ex
main :: IO ()
main = runInputT defaultSettings loop
where
loop = do
minput <- getInputLine "ready> "
case minput of
Nothing -> outputStrLn "Goodbye."
Just input -> (liftIO $ process input) >> loopIn under 100 lines of code, we fully defined our minimal language, including a lexer, parser, and AST builder. With this done, the executable will validate Kaleidoscope code, print out the Haskell representation of the AST, and tell us the position information for any syntax errors. For example, here is a sample interaction:
ready> def foo(x y) x+foo(y, 4.0);
Function "foo" [Var "x",Var "y"] (BinOp Plus (Var "x") (Call "foo" [Var "y",Float 4.0]))
ready> def foo(x y) x+y y;
Function "foo" [Var "x",Var "y"] (BinOp Plus (Var "x") (Var "y"))
Var "y"
ready> def foo(x y) x+y );
"<stdin>" (line 1, column 18):
unexpected ")"
expecting float, natural, "extern", "def", identifier, "(" or ";"
ready> extern sin(a);
Extern "sin" [Var "a"]
ready> ^D
Goodbye.There is a lot of room for extension here. You can define new AST nodes, extend the language in many ways, etc. In the next installment, we will describe how to generate LLVM Intermediate Representation (IR) from the AST.
Full Source
See src/chapter2 for the full source from this chapter.
Chapter 3 ( Code Generation )
This chapter illustrates how to transform the Abstract Syntax Tree, built in Chapter 2, into LLVM IR. This will demonstrate a little bit about how LLVM does things, as well as demonstrate how easy it is to use.
Haskell LLVM Bindings
The LLVM bindings for Haskell are split across two packages:
llvm-general-pure is a pure Haskell representation of the LLVM IR.
llvm-general is the FFI bindings to LLVM required for constructing the C representation of the LLVM IR and performing optimization and compilation.
llvm-general-pure does not require the LLVM libraries be available on the system.
On Hackage there is an older version of llvm bindings named llvm and llvm-base which should likely be avoided since they has not been updated since it's development a few years ago.
As an aside the GHCi can have issues with the FFI and can lead to errors when working with llvm-general. If you end up with errors like the following, then you are likely trying to use GHCi or runhaskell and it is unable to link against your LLVM library. Instead compile with standalone ghc.
Loading package llvm-general-3.3.8.2
... linking
... ghc: /usr/lib/llvm-3.3/lib/libLLVMSupport.a: unknown symbol `_ZTVN4llvm14error_categoryE'
ghc: unable to load package `llvm-general-3.3.8.2'Code Generation Setup
We start with a new Haskell module Codegen.hs which will hold the pure code generation logic that we'll use to drive building llvm-general's AST. For simplicity's sake we'll insist that all variables be of a single type, the double type.
double :: Type
double = FloatingPointType 64 IEEETo start we create a new record type to hold the internal state of our code generator as we walk the AST. We'll use two records, one for the toplevel module code generation and one for basic blocks inside of function definitions.
type SymbolTable = [(String, Operand)]
data CodegenState
= CodegenState {
currentBlock :: Name -- Name of the active block to append to
, blocks :: Map.Map Name BlockState -- Blocks for function
, symtab :: SymbolTable -- Function scope symbol table
, blockCount :: Int -- Count of basic blocks
, count :: Word -- Count of unnamed instructions
, names :: Names -- Name Supply
} deriving Show
data BlockState
= BlockState {
idx :: Int -- Block index
, stack :: [Named Instruction] -- Stack of instructions
, term :: Maybe (Named Terminator) -- Block terminator
} deriving ShowWe'll hold the state of the code generator inside of Codegen State monad, the Codegen monad contains a map of block names to their BlockState representation.
newtype Codegen a = Codegen { runCodegen :: State CodegenState a }
deriving (Functor, Applicative, Monad, MonadState CodegenState )At the top level we'll create a LLVM State monad which will hold all code a for the LLVM module and upon evaluation will emit llvm-general Module containing the AST. We'll append to the list of definitions in the AST.Module field moduleDefinitions.
newtype LLVM a = LLVM { unLLVM :: State AST.Module a }
deriving (Functor, Applicative, Monad, MonadState AST.Module )
runLLVM :: AST.Module -> LLVM a -> AST.Module
runLLVM = flip (execState . unLLVM)
emptyModule :: String -> AST.Module
emptyModule label = defaultModule { moduleName = label }
addDefn :: Definition -> LLVM ()
addDefn d = do
defs <- gets moduleDefinitions
modify $ \s -> s { moduleDefinitions = defs ++ [d] }Inside of our module we'll need to insert our toplevel definitions. For our purposes this will consist entirely of local functions and external function declarations.
define :: Type -> String -> [(Type, Name)] -> [BasicBlock] -> LLVM ()
define retty label argtys body = addDefn $
GlobalDefinition $ functionDefaults {
name = Name label
, parameters = ([Parameter ty nm [] | (ty, nm) <- argtys], False)
, returnType = retty
, basicBlocks = body
}
external :: Type -> String -> [(Type, Name)] -> LLVM ()
external retty label argtys = addDefn $
GlobalDefinition $ functionDefaults {
name = Name label
, parameters = ([Parameter ty nm [] | (ty, nm) <- argtys], False)
, returnType = retty
, basicBlocks = []
}Blocks
With our monad we'll create several functions to manipulate the current block state so that we can push and pop the block "cursor" and append instructions into the current block.
entry :: Codegen Name
entry = gets currentBlock
addBlock :: String -> Codegen Name
addBlock bname = do
bls <- gets blocks
ix <- gets blockCount
nms <- gets names
let new = emptyBlock ix
(qname, supply) = uniqueName bname nms
modify $ \s -> s { blocks = Map.insert (Name qname) new bls
, blockCount = ix + 1
, names = supply
}
return (Name qname)
setBlock :: Name -> Codegen Name
setBlock bname = do
modify $ \s -> s { currentBlock = bname }
return bname
getBlock :: Codegen Name
getBlock = gets currentBlock
modifyBlock :: BlockState -> Codegen ()
modifyBlock new = do
active <- gets currentBlock
modify $ \s -> s { blocks = Map.insert active new (blocks s) }
current :: Codegen BlockState
current = do
c <- gets currentBlock
blks <- gets blocks
case Map.lookup c blks of
Just x -> return x
Nothing -> error $ "No such block: " ++ show cInstructions
Now that we have the basic infrastructure in place we'll wrap the raw llvm-general AST nodes inside a collection of helper functions to push instructions onto the stack held within our monad.
Instructions in LLVM are either numbered sequentially (%0, %1, ...) or given explicit variable names (%a, %foo, ..). For example the arguments to the following function are named values, while the result of the add instructions unnamed.
define i32 @add(i32 %a, i32 %b) {
%1 = add i32 %a, %b
ret i32 %1
}In the implementation of llvm-general both these types are represented in a sum type containing the constructors UnName and Name. For most of our purpose we will simply use numbered expressions and map them numbers to identifiers with in our symbol table. Every instruction added will increment the internal counter, to accomplish we add a fresh name supply.
fresh :: Codegen Word
fresh = do
i <- gets count
modify $ \s -> s { count = 1 + i }
return $ i + 1Throughout our code we will however refer named values within the module, these have a special data type Name for which we'll create a second name supply map which guarantees that our block names are unique. We'll also instantiate a IsString instance for this type so that Haskell can automatically perform the boilerplate coercions between String types.
type Names = Map.Map String Int
uniqueName :: String -> Names -> (String, Names)
uniqueName nm ns =
case Map.lookup nm ns of
Nothing -> (nm, Map.insert nm 1 ns)
Just ix -> (nm ++ show ix, Map.insert nm (ix+1) ns)
instance IsString Name where
fromString = Name . fromStringSince we can now work with named LLVM values we need to create several functions for referring to references of values.
local :: Name -> Operand
local = LocalReference double
externf :: Name -> Operand
externf = ConstantOperand . C.GlobalReference doubleOur function externf will emit a named value which refers to a toplevel function (@add) in our module or will refer to an externally declared function (@putchar). For instance:
declare i32 @putchar(i32)
define i32 @add(i32 %a, i32 %b) {
%1 = add i32 %a, %b
ret i32 %1
}
define void @main() {
%1 = call i32 @add(i32 0, i32 97)
call i32 @putchar(i32 %1)
ret void
}Since we'd like to refer to values on the stack by named quantities we'll implement a simple symbol table as an association list letting us assign variable names to operand quantities and subsequently look them up when used.
assign :: String -> Operand -> Codegen ()
assign var x = do
lcls <- gets symtab
modify $ \s -> s { symtab = [(var, x)] ++ lcls }
getvar :: String -> Codegen Operand
getvar var = do
syms <- gets symtab
case lookup var syms of
Just x -> return x
Nothing -> error $ "Local variable not in scope: " ++ show varNow that we have a way of naming instructions we'll create a internal function to take a llvm -general AST node and push it on the current basic block stack. We'll return the left hand side reference of the instruction. Instructions will come in two flavors, instructions and terminators. Every basic block has a unique terminator and every last basic block in a function must terminate in a ret.
instr :: Instruction -> Codegen Operand
instr ins = do
n <- fresh
blk <- current
let i = stack blk
let ref = (UnName n)
modifyBlock $ blk { stack = i ++ [ref := ins] }
return $ local ref
terminator :: Named Terminator -> Codegen (Named Terminator)
terminator trm = do
blk <- current
modifyBlock $ blk { term = Just trm }
return trmUsing the instr function we now wrap the AST nodes for basic arithmetic operations of floating point values.
fadd :: Operand -> Operand -> Codegen Operand
fadd a b = instr $ FAdd NoFastMathFlags a b []
fsub :: Operand -> Operand -> Codegen Operand
fsub a b = instr $ FSub NoFastMathFlags a b []
fmul :: Operand -> Operand -> Codegen Operand
fmul a b = instr $ FMul NoFastMathFlags a b []
fdiv :: Operand -> Operand -> Codegen Operand
fdiv a b = instr $ FDiv NoFastMathFlags a b []On top of the basic arithmetic functions we'll add the basic control flow operations which will allow us to direct the control flow between basic blocks and return values.
br :: Name -> Codegen (Named Terminator)
br val = terminator $ Do $ Br val []
cbr :: Operand -> Name -> Name -> Codegen (Named Terminator)
cbr cond tr fl = terminator $ Do $ CondBr cond tr fl []
ret :: Operand -> Codegen (Named Terminator)
ret val = terminator $ Do $ Ret (Just val) []Finally we'll add several "effect" instructions which will invoke memory and evaluation side-effects. The call instruction will simply take a named function reference and a list of arguments and evaluate it and simply invoke it at the current position. The alloca instruction will create a pointer to a stack allocated uninitialized value of the given type.
call :: Operand -> [Operand] -> Codegen Operand
call fn args = instr $ Call Nothing CC.C [] (Right fn) (toArgs args) [] []
alloca :: Type -> Codegen Operand
alloca ty = instr $ Alloca ty Nothing 0 []
store :: Operand -> Operand -> Codegen Operand
store ptr val = instr $ Store False ptr val Nothing 0 []
load :: Operand -> Codegen Operand
load ptr = instr $ Load False ptr Nothing 0 []From AST to IR
Now that we have the infrastructure in place we can begin ingest our AST from Syntax.hs and construct a LLVM module from it. We will create a new Emit.hs module and spread the logic across two functions. The first codegenTop will emit toplevel constructions in modules ( functions and external definitions ) and will return a LLVM monad. The last instruction on the stack we'll bind into the ret instruction to ensure and emit as the return value of the function. We'll also sequentially assign each of the named arguments from the function to a stack allocated value with a reference in our symbol table.
codegenTop :: S.Expr -> LLVM ()
codegenTop (S.Function name args body) = do
define double name fnargs bls
where
fnargs = toSig args
bls = createBlocks $ execCodegen $ do
entry <- addBlock entryBlockName
setBlock entry
forM args $ \a -> do
var <- alloca double
store var (local (AST.Name a))
assign a var
cgen body >>= ret
codegenTop (S.Extern name args) = do
external double name fnargs []
where fnargs = toSig args
codegenTop exp = do
define double "main" [] blks
where
blks = createBlocks $ execCodegen $ do
entry <- addBlock entryBlockName
setBlock entry
cgen exp >>= ret
toSig :: [String] -> [(AST.Type, AST.Name)]
toSig = map (\x -> (double, AST.Name x))The second is the expression level code generation (cgen) which will recursively walk the AST pushing instructions on the stack and changing the current block as needed. The simplest AST node is constant integers and floating point values which simply return constant values in LLVM IR.
cgen :: S.Expr -> Codegen AST.Operand
cgen (S.Float n) = return $ cons $ C.Float (F.Double n)We need to reference local variables so we'll invoke our getvar function in conjunction with a load use values. The conscious reader will intuit that this might result in an excessive amount of extraneous instructions pushing temporary values on the stack, something that we'll address later with a simple optimization pass.
cgen (S.Var x) = getvar x >>= loadFor Call we'll first evaluate each argument and then invoke the function with the values. Since our language only has double type values, this is trivial and we don't need to worry too much.
cgen (S.Call fn args) = do
largs <- mapM cgen args
call (externf (AST.Name fn)) largsFinally for our operators we'll construct a predefined association map of symbol strings to implementations of functions with the corresponding logic for the operation.
binops = Map.fromList [
("+", fadd)
, ("-", fsub)
, ("*", fmul)
, ("/", fdiv)
, ("<", lt)
]For the comparison operator we'll invoke the uitofp which will convert a unsigned integer quantity to a floating point value. LLVM requires the unsigned single bit types as the values for comparison and test operations but we prefer to work entirely with doubles where possible.
lt :: AST.Operand -> AST.Operand -> Codegen AST.Operand
lt a b = do
test <- fcmp FP.ULT a b
uitofp double testJust like the call instruction above we simply generate the code for operands and invoke the function we just looked up for the symbol.
cgen (S.BinaryOp op a b) = do
case Map.lookup op binops of
Just f -> do
ca <- cgen a
cb <- cgen b
f ca cb
Nothing -> error "No such operator"Putting everything together we find that we nice little minimal language that supports both function abstraction and basic arithmetic. The final step is to hook into LLVM bindings to generate a string representation of the LLVM IR which we'll print our the string on each action in the REPL. We'll discuss these functions in more depth in the next chapter.
codegen :: AST.Module -> [S.Expr] -> IO AST.Module
codegen mod fns = withContext $ \context ->
liftError $ withModuleFromAST context newast $ \m -> do
llstr <- moduleLLVMAssembly m
putStrLn llstr
return newast
where
modn = mapM codegenTop fns
newast = runLLVM mod modnRunning Main.hs we can observe our code generator in action.
ready> def foo(a b) a*a + 2*a*b + b*b
; ModuleID = 'my cool jit'
define double @foo(double %a, double %b) {
entry:
%0 = fmul double %a, %a
%1 = fmul double %a, 2.000000e+00
%2 = fmul double %1, %b
%3 = fadd double %0, %2
%4 = fmul double %b, %b
%5 = fadd double %4, %3
ret double %5
}
ready> def bar(a) foo(a, 4.0) + bar(31337)
define double @bar(double %a) {
entry:
%0 = alloca double
store double %a, double* %0
%1 = load double* %0
%2 = call double @foo(double %1, double 4.000000e+00)
%3 = call double @bar(double 3.133700e+04)
%4 = fadd double %2, %3
ret double %4
}Full Source
See src/chapter3 for the full source from this chapter.
Chapter 4 ( JIT and Optimizer Support )
In the previous chapter we were able to map our language Syntax into the LLVM IR and print it out to the screen. This chapter describes two new techniques: adding optimizer support to our language, and adding JIT compiler support. These additions will demonstrate how to get nice, efficient code for the Kaleidoscope language.
ASTs and Modules
We'll refer to a Module as holding the internal representation of the LLVM IR. Modules can be generated from the Haskell LLVM AST or from strings containing bitcode.
Both data types have the same name ( Module ), so as convention we will call qualify the imports of the libraries to distinguish between the two.
AST.Module: Haskell AST ModuleModule: Internal LLVM Module
llvm-general provides two important functions for converting between them. withModuleFromAST has type ErrorT since it may fail if given a malformed expression, it is important to handle both cases of the resulting Either value.
withModuleFromAST :: Context -> AST.Module -> (Module -> IO a) -> ErrorT String IO a
moduleAST :: Module -> IO AST.ModuleWe can also generate the assembly code for our given module by passing a specification of the CPU and platform information we wish to target, called the TargetMachine.
moduleAssembly :: TargetMachine -> Module -> ErrorT String IO StringRecall the so called "Bracket" pattern in Haskell for managing IO resources. llvm-general makes heavy use this pattern to manage the life-cycle of certain LLVM resources. It is very important to remember not to pass or attempt to use resources outside of the bracket as this will lead to undefined behavior and/or segfaults.
bracket :: IO a -- computation to run first ("acquire resource")
-> (a -> IO b) -- computation to run last ("release resource")
-> (a -> IO c) -- computation to run in-between
-> IO cIn addition to this we'll often be dealing with operations which can fail in an EitherT monad if given bad code. We'll often want to lift this error up the monad transformer stack with the pattern:
liftError :: ErrorT String IO a -> IO a
liftError = runErrorT >=> either fail returnTo start we'll create a runJIT function which will start with a stack of brackets. We'll then simply generate the IR and print it out to the screen.
runJIT :: AST.Module -> IO (Either String ())
runJIT mod = do
withContext $ \context ->
runErrorT $ withModuleFromAST context mod $ \m ->
s <- moduleString m
putStrLn sConstant Folding
Our demonstration for Chapter 3 is elegant and easy to extend. Unfortunately, it does not produce wonderful code. However the naive construction of the LLVM module will perform some minimal transformations to generate a module which not a literal transcription of the AST but preserves the same semantics.
The "dumb" transcription would look like:
ready> def test(x) 1+2+x
define double @test(double %x) {
entry:
%addtmp = fadd double 2.000000e+00, 1.000000e+00
%addtmp1 = fadd double %addtmp, %x
ret double %addtmp1
}The "smarter" transcription would eliminate the first line since it contains a simple constant that can be computed at compile-time.
ready> def test(x) 1+2+x
define double @test(double %x) {
entry:
%addtmp = fadd double 3.000000e+00, %x
ret double %addtmp
}Constant folding, as seen above, in particular, is a very common and very important optimization: so much so that many language implementors implement constant folding support in their AST representation. This technique is limited by the fact that it does all of its analysis inline with the code as it is built. If you take a slightly more complex example:
ready> def test(x) (1+2+x)*(x+(1+2))
define double @test(double %x) {
entry:
%addtmp = fadd double 3.000000e+00, %x
%addtmp1 = fadd double %x, 3.000000e+00
%multmp = fmul double %addtmp, %addtmp1
ret double %multmp
}In this case, the left and right hand sides of the multiplication are the same value. We'd really like to see this generate tmp = x+3; result = tmp*tmp instead of computing x+3 twice.
Unfortunately, no amount of local analysis will be able to detect and correct this. This requires two transformations: reassociation of expressions (to make the adds lexically identical) and Common Subexpression Elimination (CSE) to delete the redundant add instruction. Fortunately, LLVM provides a broad range of optimizations that we can use, in the form of “passes”.
Optimization Passes
LLVM provides many optimization passes, which do many different sorts of things and have different trade-offs. Unlike other systems, LLVM doesn't hold to the mistaken notion that one set of optimizations is right for all languages and for all situations. LLVM allows a compiler implementor to make complete decisions about what optimizations to use, in which order, and in what situation.
As a concrete example, LLVM supports both “whole module” passes, which look across as large of body of code as they can (often a whole file, but if run at link time, this can be a substantial portion of the whole program). It also supports and includes “per-function” passes which just operate on a single function at a time, without looking at other functions. For more information on passes and how they are run, see the How to Write a Pass document and the List of LLVM Passes.
For Kaleidoscope, we are currently generating functions on the fly, one at a time, as the user types them in. We aren't shooting for the ultimate optimization experience in this setting, but we also want to catch the easy and quick stuff where possible.
We won't delve too much into the details of the passes since they are better described elsewhere. We will instead just invoke the default "curated passes" with an optimization level which will perform most of the common clean-ups and a few non-trivial optimizations.
passes :: PassSetSpec
passes = defaultCuratedPassSetSpec { optLevel = Just 3 }To apply the passes we create a bracket for a PassManager and invoke runPassManager on our working module. Note that this modifies the module in-place.
runJIT :: AST.Module -> IO (Either String AST.Module)
runJIT mod = do
withContext $ \context ->
runErrorT $ withModuleFromAST context mod $ \m ->
withPassManager passes $ \pm -> do
runPassManager pm m
optmod <- moduleAST m
s <- moduleString m
putStrLn s
return optmodWith this in place, we can try our test above again:
ready> def test(x) (1+2+x)*(x+(1+2))
; ModuleID = 'my cool jit'
; Function Attrs: nounwind readnone
define double @test(double %x) #0 {
entry:
%0 = fadd double %x, 3.000000e+00
%1 = fmul double %0, %0
ret double %1
}
attributes #0 = { nounwind readnone }As expected, we now get our nicely optimized code, saving a floating point add instruction from every execution of this function. We also see some extra metadata attached to our function, which we can ignore for now, but is indicating certain properties of the function that aid in later optimization.
LLVM provides a wide variety of optimizations that can be used in certain circumstances. Some documentation about the various passes is available, but it isn't very complete. Another good source of ideas can come from looking at the passes that Clang runs to get started. The “opt” tool allows us to experiment with passes from the command line, so we can see if they do anything.
One important optimization pass is a "analysis pass" which will validate that the internal IR is well-formed. Since it quite possible (even easy!) to construct nonsensical or unsafe IR it is very good practice to validate our IR before attempting to optimize or execute it. To do we simply invoke the verify function with our active module.
runJIT :: AST.Module -> IO (Either String AST.Module)
runJIT mod = do
...
withPassManager passes $ \pm -> do
runErrorT $ verify mNow that we have reasonable code coming out of our front-end, lets talk about executing it!
Adding a JIT Compiler
Code that is available in LLVM IR can have a wide variety of tools applied to it. For example, we can run optimizations on it (as we did above), we can dump it out in textual or binary forms, we can compile the code to an assembly file (.s) for some target, or we can JIT compile it. The nice thing about the LLVM IR representation is that it is the “common currency” between many different parts of the compiler.
In this section, we'll add JIT compiler support to our interpreter. The basic idea that we want for Kaleidoscope is to have the user enter function bodies as they do now, but immediately evaluate the top-level expressions they type in. For example, if they type in “1 + 2;”, we should evaluate and print out 3. If they define a function, they should be able to call it from the command line.
In order to do this, we add another function to bracket the creation of the JIT Execution Engine. There are two provided engines: jit and mcjit. The distinction is not important for us but we will opt to use the newer mcjit.
import qualified LLVM.General.ExecutionEngine as EE
jit :: Context -> (EE.MCJIT -> IO a) -> IO a
jit c = EE.withMCJIT c optlevel model ptrelim fastins
where
optlevel = Just 2 -- optimization level
model = Nothing -- code model ( Default )
ptrelim = Nothing -- frame pointer elimination
fastins = Nothing -- fast instruction selectionThe result of the JIT compiling our function will be a C function pointer which we can call from within the JIT's process space. We need some (unsafe!) plumbing to coerce our foreign C function into a callable object from Haskell. Some care must be taken when performing these operations since we're telling Haskell to "trust us" that the pointer we hand it is actually typed as we describe it. If we don't take care with the casts we can expect undefined behavior.
foreign import ccall "dynamic" haskFun :: FunPtr (IO Double) -> (IO Double)
run :: FunPtr a -> IO Double
run fn = haskFun (castFunPtr fn :: FunPtr (IO Double))Integrating this with our function from above we can now manifest our IR as executable code inside the ExecutionEngine and pass the resulting native types to and from the Haskell runtime.
runJIT :: AST.Module -> IO (Either String ())
runJIT mod = do
...
jit context $ \executionEngine ->
...
EE.withModuleInEngine executionEngine m $ \ee -> do
mainfn <- EE.getFunction ee (AST.Name "main")
case mainfn of
Just fn -> do
res <- run fn
putStrLn $ "Evaluated to: " ++ show res
Nothing -> return ()Having to statically declare our function pointer type is rather inflexible, if we wish to extend to this to be more flexible a library like libffi is very useful for calling functions with argument types that can be determined at runtime.
External Functions
The JIT provides a number of other more advanced interfaces for things like freeing allocated machine code, rejit'ing functions to update them, etc. However, even with this simple code, we get some surprisingly powerful capabilities - check this out:
ready> extern sin(x)
; ModuleID = 'my cool jit'
declare double @sin(double)
ready> extern cos(x)
; ModuleID = 'my cool jit'
declare double @sin(double)
declare double @cos(double)
ready> sin(1.0)
; ModuleID = 'my cool jit'
declare double @sin(double)
declare double @cos(double)
define double @main() {
entry:
%0 = call double @sin(double 1.000000e+00)
ret double %0
}
Evaluated to: 0.8414709848078965Whoa, how does the JIT know about sin and cos? The answer is surprisingly simple: in this example, the JIT started execution of a function and got to a function call. It realized that the function was not yet JIT compiled and invoked the standard set of routines to resolve the function. In this case, there is no body defined for the function, so the JIT ended up calling dlsym("sin") on the Kaleidoscope process itself. Since "sin" is defined within the JIT's address space, it simply patches up calls in the module to call the libm version of sin directly.
The LLVM JIT provides a number of interfaces for controlling how unknown functions get resolved. It allows us to establish explicit mappings between IR objects and addresses (useful for LLVM global variables that we want to map to static tables, for example), allows us to dynamically decide on the fly based on the function name, and even allows us JIT compile functions lazily the first time they're called.
One interesting application of this is that we can now extend the language by writing arbitrary C code to implement operations. For example, if create a shared library cbits.so:
/* cbits
$ gcc -fPIC -shared cbits.c -o cbits.so
$ clang -fPIC -shared cbits.c -o cbits.so
*/
#include "stdio.h"
// putchard - putchar that takes a double and returns 0.
double putchard(double X) {
putchar((char)X);
fflush(stdout);
return 0;
}Compile this with your favorite C compiler. We can then link this into our Haskell binary by simply including it along side the rest of the Haskell source files
$ ghc cbits.so --make Main.hs -o MainNow we can produce simple output to the console by using things like: extern putchard(x); putchard(120);, which prints a lowercase 'x' on the console (120 is the ASCII code for 'x'). Similar code could be used to implement file I/O, console input, and many other capabilities in Kaleidoscope.
To bring external shared objects into the process address space we can call Haskell's bindings to the system dynamic linking loader to load external libraries. In addition if we are statically compiling our interpreter we can tell GHC to link against the shared objects explicitly by passing them in with the -l flag.
This completes the JIT and optimizer chapter of the Kaleidoscope tutorial. At this point, we can compile a non-Turing-complete programming language, optimize and JIT compile it in a user-driven way. Next up we'll look into extending the language with control flow constructs, tackling some interesting LLVM IR issues along the way.
Full Source
See src/chapter4 for the full source from this chapter.
Chapter 5 ( Control Flow )
Welcome to Chapter 5 of the Implementing a language with LLVM tutorial. Parts 1-4 described the implementation of the simple Kaleidoscope language and included support for generating LLVM IR, followed by optimizations and a JIT compiler. Unfortunately, as presented, Kaleidoscope is mostly useless: it has no control flow other than call and return. This means that we can't have conditional branches in the code, significantly limiting its power. In this episode of "build that compiler", we'll extend Kaleidoscope to have an if/then/else expression plus a simple 'for' loop.
‘if' Expressions
Extending Kaleidoscope to support if/then/else is quite straightforward. It basically requires adding lexer support for this "new" concept to the lexer, parser, AST, and LLVM code emitter. This example is nice, because it shows how easy it is to "grow" a language over time, incrementally extending it as new ideas are discovered.
Before we get going on "how" we add this extension, lets talk about "what" we want. The basic idea is that we want to be able to write this sort of thing:
def fib(x)
if x < 3 then
1
else
fib(x-1) + fib(x-2)In Kaleidoscope, every construct is an expression: there are no statements. As such, the if/then/else expression needs to return a value like any other. Since we're using a mostly functional form, we'll have it evaluate its conditional, then return the ‘then' or ‘else' value based on how the condition was resolved. This is very similar to the C "?:" expression.
The semantics of the if/then/else expression is that it evaluates the condition to a boolean equality value: 0.0 is considered to be false and everything else is considered to be true. If the condition is true, the first subexpression is evaluated and returned, if the condition is false, the second subexpression is evaluated and returned. Since Kaleidoscope allows side-effects, this behavior is important to nail down.
Now that we know what we "want", let's break this down into its constituent pieces.
To represent the new expression we add a new AST node for it:
data Expr
...
| If Expr Expr Expr
deriving (Eq, Ord, Show)We also extend our lexer definition with the new reserved names.
lexer :: Tok.TokenParser ()
lexer = Tok.makeTokenParser style
where
ops = ["+","*","-","/",";",",","<"]
names = ["def","extern","if","then","else]
style = emptyDef {
Tok.commentLine = "#"
, Tok.reservedOpNames = ops
, Tok.reservedNames = names
}Now that we have the relevant tokens coming from the lexer and we have the AST node to build, our parsing logic is relatively straightforward. First we define a new parsing function:
ifthen :: Parser Expr
ifthen = do
reserved "if"
cond <- expr
reserved "then"
tr <- expr
reserved "else"
fl <- expr
return $ If cond tr flNow that we have it parsing and building the AST, the final piece is adding LLVM code generation support. This is the most interesting part of the if/then/else example, because this is where it starts to introduce new concepts. All of the code above has been thoroughly described in previous chapters.
To motivate the code we want to produce, lets take a look at a simple example. Consider:
extern foo();
extern bar();
def baz(x) if x then foo() else bar();declare double @foo()
declare double @bar()
define double @baz(double %x) {
entry:
%ifcond = fcmp one double %x, 0.000000e+00
br i1 %ifcond, label %then, label %else
then: ; preds = %entry
%calltmp = call double @foo()
br label %ifcont
else: ; preds = %entry
%calltmp1 = call double @bar()
br label %ifcont
ifcont: ; preds = %else, %then
%iftmp = phi double [ %calltmp, %then ], [ %calltmp1, %else ]
ret double %iftmp
}To visualize the control flow graph, we can use a nifty feature of the LLVM opt tool. If we put this LLVM IR into "t.ll" and run
$ llvm-as < t.ll | opt -analyze -view-cfgA window will pop up and we'll see this graph:
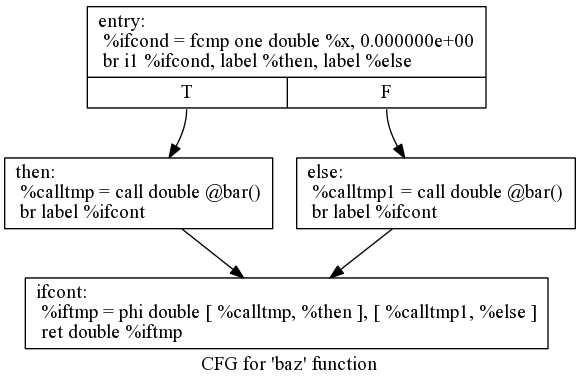
LLVM has many nice features for visualizing various graphs, but note that these are available only if your LLVM was built with Graphviz support (accomplished by having Graphviz and Ghostview installed when building LLVM).
Getting back to the generated code, it is fairly simple: the entry block evaluates the conditional expression ("x" in our case here) and compares the result to 0.0 with the fcmp one instruction (one is "Ordered and Not Equal"). Based on the result of this expression, the code jumps to either the "then" or "else" blocks, which contain the expressions for the true/false cases.
Once the then/else blocks are finished executing, they both branch back to the if.exit block to execute the code that happens after the if/then/else. In this case the only thing left to do is to return to the caller of the function. The question then becomes: how does the code know which expression to return?
The answer to this question involves an important SSA operation: the Phi operation. If you're not familiar with SSA, the Wikipedia article is a good introduction and there are various other introductions to it available on your favorite search engine. The short version is that "execution" of the Phi operation requires "remembering" which block control came from. The Phi operation takes on the value corresponding to the input control block. In this case, if control comes in from the if.then block, it gets the value of calltmp. If control comes from the if.else block, it gets the value of calltmp1.
At this point, you are probably starting to think "Oh no! This means my simple and elegant front-end will have to start generating SSA form in order to use LLVM!". Fortunately, this is not the case, and we strongly advise not implementing an SSA construction algorithm in your front-end unless there is an amazingly good reason to do so. In practice, there are two sorts of values that float around in code written for your average imperative programming language that might need Phi nodes:
- Code that involves user variables: x = 1; x = x + 1;
- Values that are implicit in the structure of your AST, such as the Phi node in this case.
In Chapter 7 of this tutorial ("mutable variables"), we'll talk about #1 in depth. For now, just believe and accept that you don't need SSA construction to handle this case. For #2, you have the choice of using the techniques that we will describe for #1, or you can insert Phi nodes directly, if convenient. In this case, it is really really easy to generate the Phi node, so we choose to do it directly.
Okay, enough of the motivation and overview, lets generate code!
In order to generate code for this, we implement the Codegen method for If node:
cgen (S.If cond tr fl) = do
ifthen <- addBlock "if.then"
ifelse <- addBlock "if.else"
ifexit <- addBlock "if.exit"
-- %entry
------------------
cond <- cgen cond
test <- fcmp FP.ONE false cond
cbr test ifthen ifelse -- Branch based on the condition
-- if.then
------------------
setBlock ifthen
trval <- cgen tr -- Generate code for the true branch
br ifexit -- Branch to the merge block
ifthen <- getBlock
-- if.else
------------------
setBlock ifelse
flval <- cgen fl -- Generate code for the false branch
br ifexit -- Branch to the merge block
ifelse <- getBlock
-- if.exit
------------------
setBlock ifexit
phi double [(trval, ifthen), (flval, ifelse)]We start by creating three blocks.
ifthen <- addBlock "if.then"
ifelse <- addBlock "if.else"
ifexit <- addBlock "if.exit"Next emit the expression for the condition, then compare that value to zero to get a truth value as a 1-bit (i.e. bool) value. We end this entry block by emitting the conditional branch that chooses between them the two cases.
test <- fcmp FP.ONE false cond
cbr test ifthen ifelse -- Branch based on the conditionAfter the conditional branch is inserted, we move switch blocks to start inserting into the if.then block.
setBlock ifthenWe recursively codegen the tr expression from the AST. To finish off the if.then block, we create an unconditional branch to the merge block. One interesting (and very important) aspect of the LLVM IR is that it requires all basic blocks to be "terminated" with a control flow instruction such as return or branch. This means that all control flow, including fallthroughs must be made explicit in the LLVM IR. If we violate this rule, the verifier will emit an error.
trval <- cgen tr -- Generate code for the true branch
br ifexit -- Branch to the merge block
ifthen <- getBlock -- Get the current blockThe final line here is quite subtle, but is very important. The basic issue is that when we create the Phi node in the merge block, we need to set up the block/value pairs that indicate how the Phi will work. Importantly, the Phi node expects to have an entry for each predecessor of the block in the CFG. Why then, are we getting the current block when we just set it block 3 lines above? The problem is that theifthen expression may actually itself change the block that the Builder is emitting into if, for example, it contains a nested "if/then/else" expression. Because calling cgen recursively could arbitrarily change the notion of the current block, we are required to get an up-to-date value for code that will set up the Phi node.
setBlock ifelse
flval <- cgen fl -- Generate code for the false branch
br ifexit -- Branch to the merge block
ifelse <- getBlockCode generation for the if.else block is basically identical to codegen for the if.then block.
setBlock ifexit
phi double [(trval, ifthen), (flval, ifelse)]The first line changes the insertion point so that newly created code will go into the if.exit block. Once that is done, we need to create the Phi node and set up the block/value pairs for the Phi.
Finally, the cgen function returns the phi node as the value computed by the if/then/else expression. In our example above, this returned value will feed into the code for the top-level function, which will create the return instruction.
Overall, we now have the ability to execute conditional code in Kaleidoscope. With this extension, Kaleidoscope is a fairly complete language that can calculate a wide variety of numeric functions. Next up we'll add another useful expression that is familiar from non-functional languages...
‘for' Loop Expressions
Now that we know how to add basic control flow constructs to the language, we have the tools to add more powerful things. Lets add something more aggressive, a ‘for' expression:
extern putchard(char)
def printstar(n)
for i = 1, i < n, 1.0 in
putchard(42); # ascii 42 = '*'
# print 100 '*' characters
printstar(100);This expression defines a new variable (i in this case) which iterates from a starting value, while the condition (i < n in this case) is true, incrementing by an optional step value (1.0 in this case). While the loop is true, it executes its body expression. Because we don't have anything better to return, we'll just define the loop as always returning 0.0. In the future when we have mutable variables, it will get more useful.
To get started, we again extend our lexer with new reserved names "for" and "in".
lexer :: Tok.TokenParser ()
lexer = Tok.makeTokenParser style
where
ops = ["+","*","-","/",";",",","<"]
names = ["def","extern","if","then","else","in","for"]
style = emptyDef {
Tok.commentLine = "#"
, Tok.reservedOpNames = ops
, Tok.reservedNames = names
}As before, lets talk about the changes that we need to Kaleidoscope to support this. The AST node is just as simple. It basically boils down to capturing the variable name and the constituent expressions in the node.
data Expr
...
| For Name Expr Expr Expr Expr
deriving (Eq, Ord, Show)The parser code captures a named value for the iterator variable and the four expressions objects for the parameters of the loop parameters.
for :: Parser Expr
for = do
reserved "for"
var <- identifier
reservedOp "="
start <- expr
reservedOp ","
cond <- expr
reservedOp ","
step <- expr
reserved "in"
body <- expr
return $ For var start cond step bodyNow we get to the good part: the LLVM IR we want to generate for this thing. With the simple example above, we get this LLVM IR (note that this dump is generated with optimizations disabled for clarity):
declare double @putchard(double)
define double @printstar(double %n) {
entry:
br label %loop
loop:
%i = phi double [ 1.000000e+00, %entry ], [ %nextvar, %loop ]
%calltmp = call double @putchard(double 4.200000e+01)
%nextvar = fadd double %i, 1.000000e+00
%cmptmp = fcmp ult double %i, %n
%booltmp = uitofp i1 %cmptmp to double
%loopcond = fcmp one double %booltmp, 0.000000e+00
br i1 %loopcond, label %loop, label %afterloop
afterloop:
ret double 0.000000e+00
}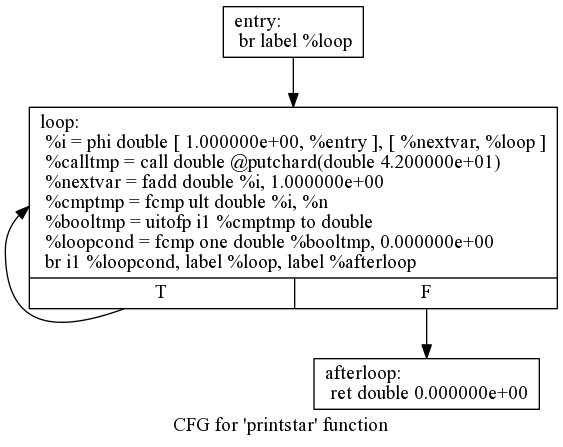
The code to generate this is only slightly more complicated than the above "if" statement.
cgen (S.For ivar start cond step body) = do
forloop <- addBlock "for.loop"
forexit <- addBlock "for.exit"
-- %entry
------------------
i <- alloca double
istart <- cgen start -- Generate loop variable initial value
stepval <- cgen step -- Generate loop variable step
store i istart -- Store the loop variable initial value
assign ivar i -- Assign loop variable to the variable name
br forloop -- Branch to the loop body block
-- for.loop
------------------
setBlock forloop
cgen body -- Generate the loop body
ival <- load i -- Load the current loop iteration
inext <- fadd ival stepval -- Increment loop variable
store i inext
cond <- cgen cond -- Generate the loop condition
test <- fcmp FP.ONE false cond -- Test if the loop condition is True ( 1.0 )
cbr test forloop forexit -- Generate the loop conditionThe first step is to set up the LLVM basic block for the start of the loop body. In the case above, the whole loop body is one block, but remember that the generating code for the body of the loop could consist of multiple blocks (e.g. if it contains an if/then/else or a for/in expression).
forloop <- addBlock "for.loop"
forexit <- addBlock "for.exit"Next we allocate the iteration variable and generate the code for the constant initial value and step.
i <- alloca double
istart <- cgen start -- Generate loop variable initial value
stepval <- cgen step -- Generate loop variable stepNow the code starts to get more interesting. Our ‘for' loop introduces a new variable to the symbol table. This means that our symbol table can now contain either function arguments or loop variables. Once the loop variable is set into the symbol table, the code recursively codegen's the body. This allows the body to use the loop variable: any references to it will naturally find it in the symbol table.
store i istart -- Store the loop variable initial value
assign ivar i -- Assign loop variable to the variable name
br forloop -- Branch to the loop body blockNow that the "preheader" for the loop is set up, we switch to emitting code for the loop body.
setBlock forloop
cgen body -- Generate the loop bodyThe body will contain the iteration variable scoped with it's code generation. After loading it's current state we increment it by the step value and store the value.
ival <- load i -- Load the current loop iteration
inext <- fadd ival stepval -- Increment loop variable
store i inextFinally, we evaluate the exit test of the loop, and conditionally either branch back to the same block or exit the loop.
cond <- cgen cond -- Generate the loop condition
test <- fcmp FP.ONE false cond -- Test if the loop condition is True ( 1.0 )
cbr test forloop forexit -- Generate the loop conditionFinally, code generation of the for loop always returns 0.0. Also note that the loop variable remains in scope even after the function exits.
setBlock forexit
return zeroWe can now generate the assembly for our printstar function, for example the body of our function will generate code like the following on x86.
printstar: # @printstar
.cfi_startproc
# BB#0: # %entry
subq $24, %rsp
.Ltmp1:
.cfi_def_cfa_offset 32
vmovsd %xmm0, 8(%rsp) # 8-byte Spill
vmovsd .LCPI0_0(%rip), %xmm0
vmovapd %xmm0, %xmm1
.align 16, 0x90
.LBB0_1: # %loop
# =>This Inner Loop Header: Depth=1
vmovsd %xmm1, 16(%rsp) # 8-byte Spill
vmovsd .LCPI0_1(%rip), %xmm0
callq putchard
vmovsd 16(%rsp), %xmm1 # 8-byte Reload
vucomisd 8(%rsp), %xmm1 # 8-byte Folded Reload
sbbl %eax, %eax
andl $1, %eax
vcvtsi2sd %eax, %xmm0, %xmm0
vaddsd .LCPI0_0(%rip), %xmm1, %xmm1
vucomisd .LCPI0_2, %xmm0
jne .LBB0_1
# BB#2: # %afterloop
vxorpd %xmm0, %xmm0, %xmm0
addq $24, %rsp
retFull Source
See src/chapter5 for the full source from this chapter.
Chapter 6 ( Operators )
Welcome to Chapter 6 of the "Implementing a language with LLVM" tutorial. At this point in our tutorial, we now have a fully functional language that is fairly minimal, but also useful. There is still one big problem with it, however. Our language doesn't have many useful operators (like division, logical negation, or even any comparisons besides less-than).
This chapter of the tutorial takes a wild digression into adding user-defined operators to the simple and beautiful Kaleidoscope language. This digression now gives us a simple and ugly language in some ways, but also a powerful one at the same time. One of the great things about creating our own language is that we get to decide what is good or bad. In this tutorial we'll assume that it is okay to use this as a way to show some interesting parsing techniques.
At the end of this tutorial, we'll run through an example Kaleidoscope application that renders the Mandelbrot set. This gives an example of what we can build with Kaleidoscope and its feature set.
User-defined Operators
The "operator overloading" that we will add to Kaleidoscope is more general than languages like C++. In C++, we are only allowed to redefine existing operators: we can't programatically change the grammar, introduce new operators, change precedence levels, etc. In this chapter, we will add this capability to Kaleidoscope, which will let the user round out the set of operators that are supported.
The two specific features we'll add are programmable unary operators (right now, Kaleidoscope has no unary operators at all) as well as binary operators. An example of this is:
# Logical unary not.
def unary!(v)
if v then
0
else
1;
# Define > with the same precedence as <.
def binary> 10 (LHS RHS)
RHS < LHS;
# Binary "logical or", (note that it does not "short circuit")
def binary| 5 (LHS RHS)
if LHS then
1
else if RHS then
1
else
0;
# Define = with slightly lower precedence than relationals.
def binary= 9 (LHS RHS)
!(LHS < RHS | LHS > RHS);Many languages aspire to being able to implement their standard runtime library in the language itself. In Kaleidoscope, we can implement significant parts of the language in the library!
We will break down implementation of these features into two parts: implementing support for user-defined binary operators and adding unary operators.
Binary Operators
We extend the lexer with two new keywords for "binary" and "unary" toplevel definitions.
lexer :: Tok.TokenParser ()
lexer = Tok.makeTokenParser style
where
ops = ["+","*","-","/",";","=",",","<",">","|",":"]
names = ["def","extern","if","then","else","in","for"
,"binary", "unary"]
style = emptyDef {
Tok.commentLine = "#"
, Tok.reservedOpNames = ops
, Tok.reservedNames = names
}Parsec has no default function to parse "any symbolic" string, but it can be added simply by defining an operator new token.
operator :: Parser String
operator = do
c <- Tok.opStart emptyDef
cs <- many $ Tok.opLetter emptyDef
return (c:cs)Using this we can then parse any binary expression. By default all our operators will be left-associative and have equal precedence, except for the bulletins we provide. A more general system would allow the parser to have internal state about the known precedences of operators before parsing. Without predefined precedence values we'll need to disambiguate expressions with parentheses.
binop = Ex.Infix (BinaryOp <$> op) Ex.AssocLeftUsing the expression parser we can extend our table of operators with the "binop" class of custom operators. Note that this will match any and all operators even at parse-time, even if there is no corresponding definition.
binops = [[binary "*" Ex.AssocLeft,
binary "/" Ex.AssocLeft]
,[binary "+" Ex.AssocLeft,
binary "-" Ex.AssocLeft]
,[binary "<" Ex.AssocLeft]]
expr :: Parser Expr
expr = Ex.buildExpressionParser (binops ++ [[binop]]) factorThe extensions to the AST consist of adding new toplevel declarations for the operator definitions.
data Expr =
...
| BinaryOp Name Expr Expr
| UnaryOp Name Expr
| BinaryDef Name [Name] Expr
| UnaryDef Name [Name] ExprThe parser extension is straightforward and essentially a function definition with a few slight change. Note that we capture the string value of the operator as given to us by the parser.
binarydef :: Parser Expr
binarydef = do
reserved "def"
reserved "binary"
o <- op
prec <- int
args <- parens $ many identifier
body <- expr
return $ BinaryDef o args bodyTo generate code we'll implement two extensions to our existing code generator. At the toplevel we'll emit the BinaryDef declarations as simply create a normal function with the name "binary" suffixed with the operator.
codegenTop (S.BinaryDef name args body) =
codegenTop $ S.Function ("binary" ++ name) args bodyNow for our binary operator instead of failing with the presence of a binary operator not declared in our binops list, we instead create a call to a named "binary" function with the operator name.
cgen (S.BinaryOp op a b) = do
case Map.lookup op binops of
Just f -> do
ca <- cgen a
cb <- cgen b
f ca cb
Nothing -> cgen (S.Call ("binary" ++ op) [a,b])Unary Operators
For unary operators we implement the same strategy as binary operators. We add a parser for unary operators simply as a Prefix operator matching any symbol.
unop = Ex.Prefix (UnaryOp <$> op)We add this to the expression parser like above.
expr :: Parser Expr
expr = Ex.buildExpressionParser (binops ++ [[unop], [binop]]) factorThe parser extension for the toplevel unary definition is precisely the same as function syntax except prefixed with the "unary" keyword.
unarydef :: Parser Expr
unarydef = do
reserved "def"
reserved "unary"
o <- op
args <- parens $ many identifier
body <- expr
return $ UnaryDef o args bodyFor toplevel declarations we'll simply emit a function with the convention that the name is prefixed with the word "unary". For example ("unary!", "unary-").
codegenTop (S.UnaryDef name args body) =
codegenTop $ S.Function ("unary" ++ name) args bodyUp until now we have not have had any unary operators so code generation we will simply always search for an implementation as a function.
cgen (S.UnaryOp op a) = do
cgen $ S.Call ("unary" ++ op) [a]That's it for unary operators, quite easy indeed!
Kicking the Tires
It is somewhat hard to believe, but with a few simple extensions we’ve covered in the last chapters, we have grown a real-ish language. With this, we can do a lot of interesting things, including I/O, math, and a bunch of other things. For example, we can now add a nice sequencing operator (printd is defined to print out the specified value and a newline):
ready> extern printd(x)
declare double @printd(double)
ready> def binary : 1 (x y) 0;
..
ready> printd(123) : printd(456) : printd(789);
123.000000
456.000000
789.000000
Evaluated to 0.000000We can also define a bunch of other "primitive" operations, such as:
# Logical unary not.
def unary!(v)
if v then
0
else
1;
# Unary negate.
def unary-(v)
0-v;
# Define > with the same precedence as <.
def binary> 10 (LHS RHS)
RHS < LHS;
# Binary logical or, which does not short circuit.
def binary| 5 (LHS RHS)
if LHS then
1
else if RHS then
1
else
0;
# Binary logical and, which does not short circuit.
def binary& 6 (LHS RHS)
if !LHS then
0
else
!!RHS;
# Define = with slightly lower precedence than relationals.
def binary = 9 (LHS RHS)
!(LHS < RHS | LHS > RHS);
# Define ':' for sequencing: as a low-precedence operator that ignores operands
# and just returns the RHS.
def binary : 1 (x y) y;Given the previous if/then/else support, we can also define interesting functions for I/O. For example, the following prints out a character whose "density" reflects the value passed in: the lower the value, the denser the character:
ready>
extern putchard(char)
def printdensity(d)
if d > 8 then
putchard(32) # ' '
else if d > 4 then
putchard(46) # '.'
else if d > 2 then
putchard(43) # '+'
else
putchard(42); # '*'
...
ready> printdensity(1): printdensity(2): printdensity(3):
printdensity(4): printdensity(5): printdensity(9):
putchard(10);
**++.
Evaluated to 0.000000The Mandelbrot set is a set of two dimensional points generated by the complex function z = z2 + c whose boundary forms a fractal.
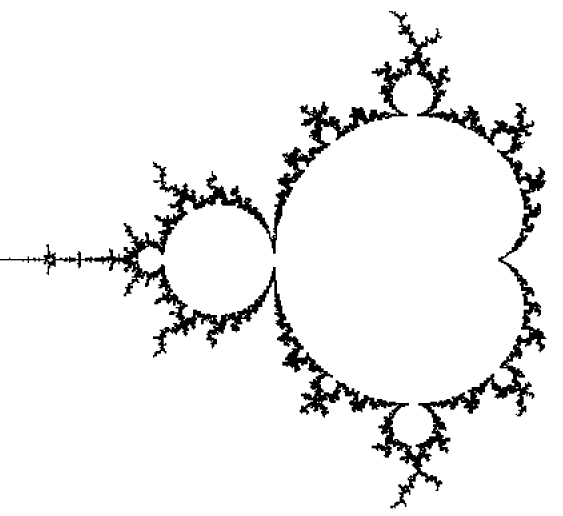
Based on our simple primitive operations defined above, we can start to define more interesting things. For example, here's a little function that solves for the number of iterations it takes a function in the complex plane to converge:
# Determine whether the specific location diverges.
# Solve for z = z^2 + c in the complex plane.
def mandelconverger(real imag iters creal cimag)
if iters > 255 | (real*real + imag*imag > 4) then
iters
else
mandelconverger(real*real - imag*imag + creal,
2*real*imag + cimag,
iters+1, creal, cimag);
# Return the number of iterations required for the iteration to escape
def mandelconverge(real imag)
mandelconverger(real, imag, 0, real, imag);Our mandelconverge function returns the number of iterations that it takes for a complex orbit to escape, saturating to 255. This is not a very useful function by itself, but if we plot its value over a two-dimensional plane, we can see the Mandelbrot set. Given that we are limited to using putchard here, our amazing graphical output is limited, but we can whip together something using the density plotter above:
# Compute and plot the mandelbrot set with the specified 2 dimensional range
# info.
def mandelhelp(xmin xmax xstep ymin ymax ystep)
for y = ymin, y < ymax, ystep in (
(for x = xmin, x < xmax, xstep in
printdensity(mandelconverge(x,y)))
: putchard(10)
);
# mandel - This is a convenient helper function for plotting the mandelbrot set
# from the specified position with the specified Magnification.
def mandel(realstart imagstart realmag imagmag)
mandelhelp(realstart, realstart+realmag*78, realmag,
imagstart, imagstart+imagmag*40, imagmag);Given this, we can try plotting out the mandelbrot set! Lets try it out:
******************************************************************************
******************************************************************************
****************************************++++++********************************
************************************+++++...++++++****************************
*********************************++++++++.. ...+++++**************************
*******************************++++++++++.. ..+++++*************************
******************************++++++++++. ..++++++************************
****************************+++++++++.... ..++++++***********************
**************************++++++++....... .....++++**********************
*************************++++++++. . ... .++*********************
***********************++++++++... ++*********************
*********************+++++++++.... .+++********************
******************+++..+++++.... ..+++*******************
**************++++++. .......... +++*******************
***********++++++++.. .. .++*******************
*********++++++++++... .++++******************
********++++++++++.. .++++******************
*******++++++..... ..++++******************
*******+........ ...++++******************
*******+... .... ...++++******************
*******+++++...... ..++++******************
*******++++++++++... .++++******************
*********++++++++++... ++++******************
**********+++++++++.. .. ..++*******************
*************++++++.. .......... +++*******************
******************+++...+++..... ..+++*******************
*********************+++++++++.... ..++********************
***********************++++++++... +++********************
*************************+++++++.. . ... .++*********************
**************************++++++++....... ......+++**********************
****************************+++++++++.... ..++++++***********************
*****************************++++++++++.. ..++++++************************
*******************************++++++++++.. ...+++++*************************
*********************************++++++++.. ...+++++**************************
***********************************++++++....+++++****************************
***************************************++++++++*******************************
******************************************************************************
******************************************************************************
******************************************************************************
******************************************************************************At this point, you may be starting to realize that Kaleidoscope is a real and powerful language. It may not be self-similar :), but it can be used to plot things that are!
With this, we conclude the "adding user-defined operators" chapter of the tutorial. We have successfully augmented our language, adding the ability to extend the language in the library, and we have shown how this can be used to build a simple but interesting end-user application in Kaleidoscope. At this point, Kaleidoscope can build a variety of applications that are functional and can call functions with side-effects, but it can't actually define and mutate a variable itself.
Strikingly, variable mutation is an important feature of imperative languages, and it is not at all obvious how to add support for mutable variables without having to add an "SSA construction" phase to our front-end. In the next chapter, we will describe how we can add variable mutation without building SSA in our front-end.
Full Source
See src/chapter6 for the full source from this chapter.
Chapter 7 ( Mutable Variables )
Welcome to Chapter 7 of the "Implementing a language with LLVM" tutorial. In chapters 1 through 6, we've built a very respectable, albeit simple, functional programming language. In our journey, we learned some parsing techniques, how to build and represent an AST, how to build LLVM IR, and how to optimize the resultant code as well as JIT compile it.
While Kaleidoscope is interesting as a functional language, the fact that it is functional makes it "too easy" to generate LLVM IR for it. In particular, a functional language makes it very easy to build LLVM IR directly in SSA form. Since LLVM requires that the input code be in SSA form, this is a very nice property and it is often unclear to newcomers how to generate code for an imperative language with mutable variables.
The short (and happy) summary of this chapter is that there is no need for our front-end to build SSA form: LLVM provides highly tuned and well tested support for this, though the way it works is a bit unexpected for some.
Why is this a hard problem?
To understand why mutable variables cause complexities in SSA construction, consider this extremely simple C example:
int G, H;
int test(_Bool Condition) {
int X;
if (Condition)
X = G;
else
X = H;
return X;
}In this case, we have the variable "X", whose value depends on the path executed in the program. Because there are two different possible values for X before the return instruction, a Phi node is inserted to merge the two values. The LLVM IR that we want for this example looks like this:
@G = weak global i32 0 ; type of @G is i32*
@H = weak global i32 0 ; type of @H is i32*
define i32 @test(i1 %Condition) {
entry:
br i1 %Condition, label %cond_true, label %cond_false
cond_true:
%X.0 = load i32* @G
br label %cond_next
cond_false:
%X.1 = load i32* @H
br label %cond_next
cond_next:
%X.2 = phi i32 [ %X.1, %cond_false ], [ %X.0, %cond_true ]
ret i32 %X.2
}The control flow graph for the above IR:
In this example, the loads from the G and H global variables are explicit in the LLVM IR, and they live in the then/else branches of the if statement (cond_true/cond_false). In order to merge the incoming values, the X.2 phi node in the cond_next block selects the right value to use based on where control flow is coming from: if control flow comes from the cond_false block, X.2 gets the value of X.1. Alternatively, if control flow comes from cond_true, it gets the value of X.0. The intent of this chapter is not to explain the details of SSA form. For more information, see one of the many online references.
The question for this article is "who places the phi nodes when lowering assignments to mutable variables?". The issue here is that LLVM requires that its IR be in SSA form: there is no "non-SSA" mode for it. However, SSA construction requires non-trivial algorithms and data structures, so it is inconvenient and wasteful for every front-end to have to reproduce this logic.
Memory in LLVM
The ‘trick' here is that while LLVM does require all register values to be in SSA form, it does not require (or permit) memory objects to be in SSA form. In the example above, note that the loads from G and H are direct accesses to G and H: they are not renamed or versioned. This differs from some other compiler systems, which do try to version memory objects. In LLVM, instead of encoding dataflow analysis of memory into the LLVM IR, it is handled with Analysis Passes which are computed on demand.
With this in mind, the high-level idea is that we want to make a stack variable (which lives in memory, because it is on the stack) for each mutable object in a function. To take advantage of this trick, we need to talk about how LLVM represents stack variables.
In LLVM, all memory accesses are explicit with load/store instructions, and it is carefully designed not to have (or need) an "address-of" operator. Notice how the type of the @G/@H global variables is actually i32* even though the variable is defined as i32. What this means is that @G defines space for an i32 in the global data area, but its name actually refers to the address for that space. Stack variables work the same way, except that instead of being declared with global variable definitions, they are declared with the LLVM alloca instruction:
define i32 @example() {
entry:
%X = alloca i32 ; type of %X is i32*.
...
%tmp = load i32* %X ; load the stack value %X from the stack.
%tmp2 = add i32 %tmp, 1 ; increment it
store i32 %tmp2, i32* %X ; store it back
...This code shows an example of how we can declare and manipulate a stack variable in the LLVM IR. Stack memory allocated with the alloca instruction is fully general: we can pass the address of the stack slot to functions, we can store it in other variables, etc. In our example above, we could rewrite the example to use the alloca technique to avoid using a Phi node:
@G = weak global i32 0 ; type of @G is i32*
@H = weak global i32 0 ; type of @H is i32*
define i32 @test(i1 %Condition) {
entry:
%X = alloca i32
br i1 %Condition, label %cond_true, label %cond_false
cond_true:
%X.0 = load i32* @G
store i32 %X.0, i32* %X
br label %cond_next
cond_false:
%X.1 = load i32* @H
store i32 %X.1, i32* %X
br label %cond_next
cond_next:
%X.2 = load i32* %X
ret i32 %X.2
}With this, we have discovered a way to handle arbitrary mutable variables without the need to create Phi nodes at all:
- Each mutable variable becomes a stack allocation.
- Each read of the variable becomes a load from the stack.
- Each update of the variable becomes a store to the stack.
- Taking the address of a variable just uses the stack address directly.
While this solution has solved our immediate problem, it introduced another one: we have now apparently introduced a lot of stack traffic for very simple and common operations, a major performance problem. Fortunately for us, the LLVM optimizer has a highly-tuned optimization pass named "mem2reg" that handles this case, promoting allocas like this into SSA registers, inserting Phi nodes as appropriate. If we run this example through the pass, for example, we'll get:
$ llvm-as < example.ll | opt -mem2reg | llvm-dis
@G = weak global i32 0
@H = weak global i32 0
define i32 @test(i1 %Condition) {
entry:
br i1 %Condition, label %cond_true, label %cond_false
cond_true:
%X.0 = load i32* @G
br label %cond_next
cond_false:
%X.1 = load i32* @H
br label %cond_next
cond_next:
%X.01 = phi i32 [ %X.1, %cond_false ], [ %X.0, %cond_true ]
ret i32 %X.01
}We say a block "A" dominates a different block "B" in the control flow graph if it's impossible to reach "B" without passing through "A", equivalently "A" is the dominator of "B". The mem2reg pass implements the standard "iterated dominance frontier" algorithm for constructing SSA form and has a number of optimizations that speed up (very common) degenerate cases.
The mem2reg optimization pass is the answer to dealing with mutable variables, and we highly recommend that you depend on it. Note that mem2reg only works on variables in certain circumstances:
- mem2reg is alloca-driven: it looks for allocas and if it can handle them, it promotes them. It does not apply to global variables or heap allocations.
- mem2reg only looks for alloca instructions in the entry block of the function. Being in the entry block guarantees that the alloca is only executed once, which makes analysis simpler.
- mem2reg only promotes allocas whose uses are direct loads and stores. If the address of the stack object is passed to a function, or if any funny pointer arithmetic is involved, the alloca will not be promoted.
- mem2reg only works on allocas of first class values (such as pointers, scalars and vectors), and only if the array size of the allocation is 1 (or missing in the .ll file).
- mem2reg is not capable of promoting structs or arrays to registers. Note that the "scalarrepl" pass is more powerful and can promote structs, "unions", and arrays in many cases.
All of these properties are easy to satisfy for most imperative languages, and we'll illustrate it below with Kaleidoscope. The final question you may be asking is: should I bother with this nonsense for my front-end? Wouldn't it be better if I just did SSA construction directly, avoiding use of the mem2reg optimization pass? In short, we strongly recommend that you use this technique for building SSA form, unless there is an extremely good reason not to. Using this technique is:
- Proven and well tested: clang uses this technique for local mutable variables. As such, the most common clients of LLVM are using this to handle a bulk of their variables. You can be sure that bugs are found fast and fixed early.
- Extremely Fast: mem2reg has a number of special cases that make it fast in common cases as well as fully general. For example, it has fast-paths for variables that are only used in a single block, variables that only have one assignment point, good heuristics to avoid insertion of unneeded phi nodes, etc.
- Needed for debug info generation: Debug information in LLVM relies on having the address of the variable exposed so that debug info can be attached to it. This technique dovetails very naturally with this style of debug info.
If nothing else, this makes it much easier to get our front-end up and running, and is very simple to implement. Lets extend Kaleidoscope with mutable variables now!
Mutable Variables
Now that we know the sort of problem we want to tackle, lets see what this looks like in the context of our little Kaleidoscope language. We're going to add two features:
- The ability to mutate variables with the ‘=' operator.
- The ability to define new variables.
While the first item is really what this is about, we only have variables for incoming arguments as well as for induction variables, and redefining those only goes so far :). Also, the ability to define new variables is a useful thing regardless of whether we will be mutating them. Here's a motivating example that shows how we could use these:
# Define ':' for sequencing: as a low-precedence operator that ignores operands
# and just returns the RHS.
def binary : 1 (x y) y;
# Recursive fib, we could do this before.
def fib(x)
if (x < 3) then
1
else
fib(x-1)+fib(x-2);
# Iterative fib.
def fibi(x)
var a = 1, b = 1, c = 0 in
(for i = 3, i < x in
c = (a + b) :
a = b :
b = c) :
b;
# Call it.
fibi(10);At this point in Kaleidoscope’s development, it only supports variables for two things: incoming arguments to functions and the induction variable of ‘for’ loops. For consistency, we’ll allow mutation of these variables in addition to other user-defined variables. This means that these will both need memory locations.
We introduce a new var syntax which behaves much like the let notation in Haskell. We will let the user define a sequence of new variable names and inject these new variables into the symbol table.
data Expr
...
| Let Name Expr Expr
deriving (Eq, Ord, Show)The parser for it will allow for multiple declarations on a single and right fold the AST node bodies, allowing us to use variables declared earlier in the list in subsequent declarations (i.e. var x = 3, y = x + 1).
letins :: Parser Expr
letins = do
reserved "var"
defs <- commaSep $ do
var <- identifier
reservedOp "="
val <- expr
return (var, val)
reserved "in"
body <- expr
return $ foldr (uncurry Let) body defsThe code generation for this new syntax is very straight forward, we simply allocate a new reference and assign it to the name given then return the assigned value.
cgen (S.Let a b c) = do
i <- alloca double
val <- cgen b
store i val
assign a i
cgen cWe can test out this new functionality. Note that code below is unoptimized and involves several extranous instructions that would normally be optimized away by mem2reg.
ready> def main(x) var y = x + 1 in y;
; ModuleID = 'my cool jit'
define double @main(double %x) {
entry:
%0 = alloca double
store double %x, double* %0
%1 = alloca double
%2 = load double* %0
%3 = fadd double %2, 1.000000e+00
store double %3, double* %1
%4 = load double* %1
ret double %4
}
Evaluated to: 1.0Assignment
Mutation of existing variables is also quite simple. We'll add a special case to our code generator for the "=" operator to add internal logic for looking up the LHS variable and assign it the right hand side using the store operation.
cgen (S.BinaryOp "=" (S.Var var) val) = do
a <- getvar var
cval <- cgen val
store a cval
return cvalTesting this out for a trivial example we find that we can now update variables.
ready> def main(x) x = 1;
; ModuleID = 'my cool jit'
define double @main(double %x) {
entry:
%0 = alloca double
store double %x, double* %0
store double 1.000000e+00, double* %0
ret double 1.000000e+00
}
Evaluated to: 1.0Finally we can write down our Fibonacci example using mutable updates.
def fibi(x)
var a = 1, b = 1, c = 0 in
(for i = 3, i < x, 1.0 in
c = (a + b) :
a = b :
b = c
): b;
fibi(10);With this, we completed what we set out to do. Our nice iterative fib example from the intro compiles and runs just fine. The mem2reg pass optimizes all of our stack variables into SSA registers, inserting PHI nodes where needed, and our front-end remains simple: no “iterated dominance frontier” computation anywhere in sight.
define double @fibi(double %x) #0 {
entry:
br label %for.loop
for.loop: ; preds = %for.loop, %entry
%0 = phi double [ %4, %for.loop ], [ 3.000000e+00, %entry ]
%1 = phi double [ %3, %for.loop ], [ 1.000000e+00, %entry ]
%2 = phi double [ %1, %for.loop ], [ 1.000000e+00, %entry ]
%3 = fadd double %2, %1
%4 = fadd double %0, 1.000000e+00
%5 = fcmp ult double %4, %x
br i1 %5, label %for.loop, label %for.exit
for.exit: ; preds = %for.loop
%6 = call double @"binary:"(double 0.000000e+00, double %3)
ret double %6
}Running the optimizations we see that we get nicely optimal assembly code for our loop. The auto-vectorizer pass has also rewriten our naive code to used SIMD instructions which yield much faster execution.
fibi: # @fibi
# BB#0: # %entry
vmovsd .LCPI2_0(%rip), %xmm2
vmovsd .LCPI2_1(%rip), %xmm3
vmovaps %xmm2, %xmm1
vmovaps %xmm2, %xmm4
.align 16, 0x90
.LBB2_1: # %for.loop
vmovaps %xmm1, %xmm5
vaddsd %xmm4, %xmm5, %xmm1
vaddsd %xmm2, %xmm3, %xmm3
vucomisd %xmm0, %xmm3
vmovaps %xmm5, %xmm4
jb .LBB2_1
# BB#2: # %for.exit
vmovaps %xmm1, %xmm0
retFull Source
See src/chapter7 for the full source from this chapter.
Chapter 8 ( Conclusion )
Tutorial Conclusion
Welcome to the final chapter of the "Implementing a language with LLVM" tutorial. In the course of this tutorial, we have grown our little Kaleidoscope language from being a useless toy, to being a semi-interesting (but probably still useless) toy. :)
It is interesting to see how far we've come, and how little code it has taken. We built the entire lexer, parser, AST, code generator, and an interactive run-loop (with a JIT!) by-hand in under 700 lines of (non-comment/non-blank) code.
Our little language supports a couple of interesting features: it supports user defined binary and unary operators, it uses JIT compilation for immediate evaluation, and it supports a few control flow constructs with SSA construction.
Part of the idea of this tutorial was to show how easy and fun it can be to define, build, and play with languages. Building a compiler need not be a scary or mystical process! Now that we've seen some of the basics, I strongly encourage you to take the code and hack on it. For example, try adding:
- global variables - While global variables have questionable value in modern software engineering, they are often useful when putting together quick little hacks like the Kaleidoscope compiler itself. Fortunately, our current setup makes it very easy to add global variables: just have value lookup check to see if an unresolved variable is in the global variable symbol table before rejecting it.
- typed variables - Kaleidoscope currently only supports variables of type double. This gives the language a very nice elegance, because only supporting one type means that we never have to specify types. Different languages have different ways of handling this. The easiest way is to require the user to specify types for every variable definition, and record the type of the variable in the symbol table along with its Value*.
- arrays, structs, vectors, etc - Once we add types, we can start extending the type system in all sorts of interesting ways. Simple arrays are very easy and are quite useful for many different applications. Adding them is mostly an exercise in learning how the LLVM getelementptr instruction works: it is so nifty/unconventional, it has its own FAQ! If we add support for recursive types (e.g. linked lists), make sure to read the section in the LLVM Programmer's Manual that describes how to construct them.
- standard runtime - Our current language allows the user to access arbitrary external functions, and we use it for things like "printd" and "putchard". As we extend the language to add higher-level constructs, often these constructs make the most sense if they are lowered to calls into a language-supplied runtime. For example, if we add hash tables to the language, it would probably make sense to add the routines to a runtime, instead of inlining them all the way.
- memory management - Currently we can only access the stack in Kaleidoscope. It would also be useful to be able to allocate heap memory, either with calls to the standard libc malloc/free interface or with a garbage collector. If we would like to use garbage collection, note that LLVM fully supports Accurate Garbage Collection including algorithms that move objects and need to scan/update the stack.
- debugger support - LLVM supports generation of DWARF Debug info which is understood by common debuggers like GDB. Adding support for debug info is fairly straightforward. The best way to understand it is to compile some C/C++ code with "clang -g -O0" and taking a look at what it produces.
- exception handling support - LLVM supports generation of zero cost exceptions which interoperate with code compiled in other languages. You could also generate code by implicitly making every function return an error value and checking it. You could also make explicit use of setjmp/longjmp. There are many different ways to go here.
- object orientation, generics, database access, complex numbers, geometric programming, ... - Really, there is no end of crazy features that we can add to the language.
- unusual domains - We've been talking about applying LLVM to a domain that many people are interested in: building a compiler for a specific language. However, there are many other domains that can use compiler technology that are not typically considered. For example, LLVM has been used to implement OpenGL graphics acceleration, translate C++ code to ActionScript, and many other cute and clever things. Maybe you will be the first to JIT compile a regular expression interpreter into native code with LLVM? Have fun try doing something crazy and unusual. Building a language like everyone else always has, is much less fun than trying something a little crazy or off the wall and seeing how it turns out. If you get stuck or want to talk about it, feel free to email the llvmdev mailing list: it has lots of people who are interested in languages and are often willing to help out.
Chapter 9 ( Appendix )
Command Line Tools
llvm-as
The assembler transforms the human readable LLVM assembly to LLVM bitcode.
Usage:
$ clang -S -emit-llvm hello.c -c -o hello.ll
$ llvm-as hello.ll -o hello.bcllvm-dis
The disassembler transforms the LLVM bitcode to human readable LLVM assembly.
Usage:
$ clang -emit-llvm hello.c -c -o hello.bc
$ llvm-dis < hello.bc | lesslli
lli is the LLVM interpreter, which can directly execute LLVM bitcode.
Usage:
$ clang -emit-llvm hello.c -c -o hello.bc
$ lli hello.bc
$ lli -use-mcjit hello.bcllc
llc is the LLVM backend compiler, which translates LLVM bitcode to native code assembly.
Usage:
$ clang -emit-llvm hello.c -c -o hello.bc
$ llc hello.bc -o hello.s
$ cc hello.s -o hello.native
$ llc -march=x86-64 hello.bc -o hello.s
$ llc -march=arm hello.bc -o hello.sopt
opt reads LLVM bitcode, applies a series of LLVM to LLVM transformations and then outputs the resultant bitcode. opt can also be used to run a specific analysis on an input LLVM bitcode file and print out the resulting IR or bitcode.
Usage:
$ clang -emit-llvm hello.c -c -o hello.bc
$ opt -mem2reg hello.bc
$ opt -simplifycfg hello.bc
$ opt -inline hello.bc
$ opt -dce hello.bc
$ opt -analyze -view-cfg hello.bc
$ opt -bb-vectorize hello.bc
$ opt -loop-vectorize -force-vector-width=8llvm-link
llvm-link links multiple LLVM modules into a single program. Together with opt this can be used to perform link-time optimizations.
Usage:
$ llvm-link foo.ll bar.ll -o foobar.ll
$ opt -std-compile-opts -std-link-opts -O3 foobar.bc -o optimized.bc