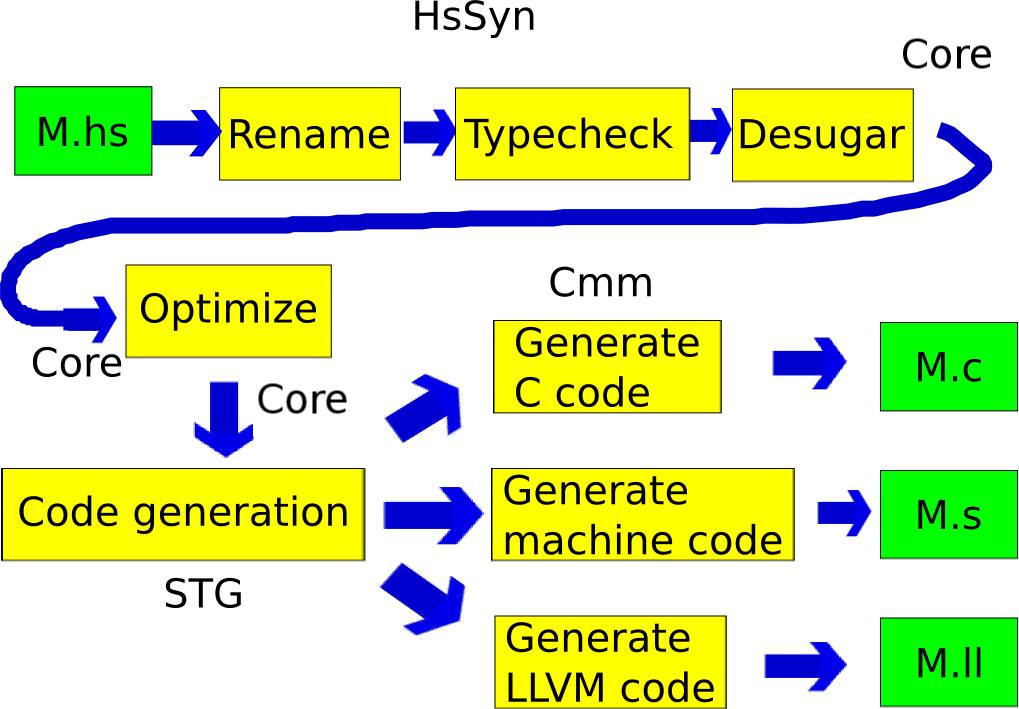
Pipeline of GHC
David Terei
(GHC Developer)
Will first give an overview of the intuitive ideas behind the compiler.
Then will go through how GHC works in terms of traditional compiler stages:
Haskell is seen as a difficult language to understand from a compilation perspective.
There are some good reasons for this:
But one reason (an annoying one) is the use of Jargon
Two good resources for dealing with unknown terminology:
Lets cover some of the terminology now:
Yes, closures, thunks and continuations are all very similar. One implementation can capture them all, however the terminology is used to capture the different use cases.

We will start though with a quick look at Core, the main intermediate language used by GHC:
Functional lazy language
It consists of only a hand full of constructs!
variables, literals, let, case, lambda abstraction, application
In general think, let means allocation, case means evaluation
For the curious, Core is technically a variant of a System FC (which is itself a variant of System F)
Basic idea of Core (and the various System <X> which are extensions of simple typed lambda calculus) is to be the smallest language needed to capture the source language. Easier to study, reason, optimize...
Useful tool for viewing Core:
cabal install ghc-core
data Expr b -- "b" for the type of binders,
= Var Id
| Lit Literal
| App (Expr b) (Arg b)
| Lam b (Expr b)
| Let (Bind b) (Expr b)
| Case (Expr b) b Type [Alt b]
| Type Type
| Cast (Expr b) Coercion
| Coercion Coercion
| Tick (Tickish Id) (Expr b)
data Bind b = NonRec b (Expr b)
| Rec [(b, (Expr b))]
type Arg b = Expr b
type Alt b = (AltCon, [b], Expr b)
data AltCon = DataAlt DataCon | LitAlt Literal | DEFAULTThe way that lazy functional languages like Haskell are implemented is through a technique called graph reduction
Its best to use the graph reduction model as an intuitive way to think about how Haskell is evaluated, the actual way GHC implements Haskell is pretty close to how an imperative language works.
f g = let x = 2 + 2
in (g x, x)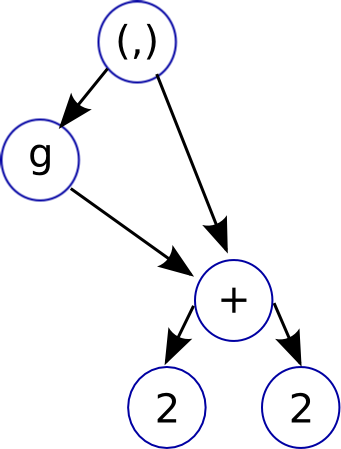
Lets now look at how Haskell is compiled to Core.
Haskell
idChar :: Char -> Char
idChar c = c
id :: a -> a
id x = x
idChar2 :: Char -> Char
idChar2 = idCore
idChar :: GHC.Types.Char -> GHC.Types.Char
[GblId, Arity=1, Caf=NoCafRefs]
idChar = \ (c :: GHC.Types.Char) -> c
id :: forall a. a -> a
id = \ (@ a) (x :: a) -> x
idChar2 :: GHC.Types.Char -> GHC.Types.Char
idChar2 = id @ GHC.Types.CharHaskell
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xsCore
map :: forall a b. (a -> b) -> [a] -> [b]
map =
\ (@ a) (@ b) (f :: a -> b) (xs :: [a]) ->
case xs of _ {
[] -> GHC.Types.[] @ b;
: y ys -> GHC.Types.: @ b (f y) (map @ a @ b f ys)
}of that captures the return value of the scrutineeHaskell
data Maybe a = Nothing | Just a
none = Nothing
some = Just (1 :: Int)Core
none :: forall a. Maybe a
none = Nothing
n :: GHC.Types.Int
n = GHC.Types.I# 1
some :: Maybe GHC.Types.Int
some = Just @ GHC.Types.Int nHaskell
dox :: Int -> Int
dox n = x * x
where x = (n + 2) * 4Core
dox :: GHC.Types.Int -> GHC.Types.Int
dox =
\ (n :: GHC.Types.Int) ->
let {
x :: GHC.Types.Int
x =
GHC.Num.* @ GHC.Types.Int GHC.Num.$fNumInt
(GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt n (GHC.Types.I# 2))
(GHC.Types.I# 4) }
in GHC.Num.* @ GHC.Types.Int GHC.Num.$fNumInt x xwhere becomes letHaskell
iff :: Bool -> a -> a -> a
iff True x _ = x
iff False _ y = yCore
iff :: forall a. GHC.Bool.Bool -> a -> a -> a
iff =
\ (@ a) (d :: GHC.Bool.Bool) (x :: a) (y :: a) ->
case d of _
GHC.Bool.False -> y
GHC.Bool.True -> xcase statementsHaskell
sum100 :: Int -> Int
sum100 n = foldr (+) 0 [1..100]Core
-- Unoptimized
sum100n = \ (n :: Int) -> * n (foldr (I# 0) (enumFromTo (I# 1) (I# 100)))
-- Optimized
sum100n = \ (n :: Int) -> GHC.Base.timesInt n sum100n1
sum100n1 = case $wgo 1 of r { __DEFAULT -> GHC.Types.I# r }
$wgo :: Int# -> Int#
$wgo = \ (w :: Int#) ->
case w of w'
__DEFAULT -> case $wgo (GHC.Prim.+# w' 1) of r
__DEFAULT -> GHC.Prim.+# w' r
100 -> 100$wgo which means 'worker'. This version works with unboxed types for efficiency.Haskell
add :: Int -> Int -> Int
add x y = x + y
add2 :: Int -> Int
add2 = add 2Core (unoptimized)
add :: GHC.Types.Int -> GHC.Types.Int -> GHC.Types.Int
add =
\ (x :: GHC.Types.Int) (y :: GHC.Types.Int) ->
GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt x y
x :: GHC.Types.Int
x = GHC.Types.I# 2
add2 :: GHC.Types.Int -> GHC.Types.Int
add2 =
\ (y :: GHC.Types.Int) ->
GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumInt x yGHC.Num.+ variant
GHC.Num.+ @ GHC.Types.Int GHC.Num.$fNumtInt means, select the (+) field from the GHC.Types.Int dictionary (which is retrieved from GHC.Num.$fNumInt) for the GHC.Num type classHaskell
add :: Int -> Int -> Int
add x y = x + y
add2 :: Int -> Int
add2 = add 2Core (optimized)
add :: GHC.Types.Int -> GHC.Types.Int -> GHC.Types.Int
Hs2Core.add = GHC.Base.plusInt
x :: GHC.Types.Int
x = GHC.Types.I# 2
add2 :: GHC.Types.Int -> GHC.Types.Int
add2 = GHC.Base.plusInt xThe function GHC.Base.plusInt is implemented as:
+ :: Int -> Int -> Int
+ = \ a b -> case a of _
I# a_ -> case b of _
I# b_ -> I# (GHC.Prim.+# a_ b_)Haskell
typeclass MyEnum a where
toId :: a -> Int
fromId :: Int -> a
instance MyEnum Int where
toId = id
fromId = id
instance (MyEnum a) => MyEnum (Maybe a) where
toId (Nothing) = 0
toId (Just n) = 1 + toId n
fromId 0 = Nothing
fromId n = Just (fromId $ n - 1)Core
toId :: forall a. MyEnum a => a -> GHC.Types.Int
toId =
\ (@ a) (d :: MyEnum a) ->
case d of _ { D:MyEnum f1 _ -> f1 }
fromId :: forall a. MyEnum a => GHC.Types.Int -> a
fromId =
\ (@ a) (d :: MyEnum a) ->
case d of _ { D:MyEnum _ f2 -> f2 }Core
$fMyEnumInt :: MyEnum GHC.Types.Int
$fMyEnumInt = D:MyEnum @ GHC.Types.Int (id @ GHC.Types.Int) (id @ GHC.Types.Int)
$fMyEnumMaybe :: forall a. MyEnum a => MyEnum (Maybe a)
$fMyEnumMaybe =
\ (@ a) ($dMyEnum_arR :: MyEnum a) ->
D:MyEnum @ (Maybe a_acF)
($fMyEnumMaybe_$ctoId @ a $dMyEnum_arR)
($fMyEnumMaybe_$cfromId @ a $dMyEnum_arR)
$fMyEnumMaybe_$ctoId :: forall a. Hs2Core.MyEnum a => Hs2Core.Maybe a -> GHC.Types.Int
$fMyEnumMaybe_$ctoId =
\ (@ a) ($dMyEnum_arR :: MyEnum a) (ds :: Maybe a) ->
case ds of _
Nothing -> GHC.Types.I# 0
Just n -> case toId @ a $dMyEnum_arR n of _
GHC.Types.I# y -> GHC.Types.I# (GHC.Prim.+# 1 y)newtype IO a = IO (State# RealWorld -> (# State# RealWorld, a #))Haskell
f :: IO ()
f = do
putStrLn "Hello World"
putStrLn "What's up today?"Core (Unoptimized)
g :: GHC.Types.IO ()
g =
GHC.Base.>> @ GHC.Types.IO GHC.Base.$fMonadIO @ () @ ()
(System.IO.putStrLn (GHC.Base.unpackCString# "Hello World"))
(System.IO.putStrLn (GHC.Base.unpackCString# "What's up today?"))Core (optimized)
f :: GHC.Prim.State# GHC.Prim.RealWorld -> (# GHC.Prim.State# GHC.Prim.RealWorld, () #)
f =
\ (world :: GHC.Prim.State# GHC.Prim.RealWorld) ->
case hPutStr2 stdout f1 True world of _
(# new_world, _ #) -> hPutStr2 stdout f2 True new_world
f1 :: [GHC.Types.Char]
f2 = GHC.Base.unpackCString# "Hello World"
f2 :: [GHC.Types.Char]
f1 = GHC.Base.unpackCString# "What's up today?"unpackCString# takes a C style string and turns it into a Haskell StringHaskell
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl' :: (a -> b -> a) -> a -> [b] -> a
forcee :: a -> b -> b
forccee = seqCore
foldl = \ (f :: a -> b -> a) (z :: a) (d :: [b]) ->
case d of _
[] -> z;
: x xs -> foldl f (f z x) xs
foldl' = \ (f :: a -> b -> a) (z :: a) (d :: [b]) ->
case d of _
[] -> z;
: x xs ->
case f z x of z'
__DEFAULT -> foldl' b f z' xs
forccee = \ (x :: a) (y :: b) -> case x of _ { __DEFAULT -> y }case statement in foldl' to force evaluationwhere statements become let statementslet and case gives you a good idea of evaluation ordercase means evaluation. (e.g seq is translated to case)let statements are allocation of closuresHopefully you have a decent idea of how Haskell is reduced to Core now. Once we have the Core IR we can do a lot of optimization work:
Rest of the optimisations GHC does are fairly specific to a functional language. Lets look at a few of them.
Fun Fact: Estimated that functional languages gain 20 - 40%
improvement from inlining Vs. imperative languages which gain 10 - 15%
In the next few slides the code Ill be showing isn't exactly Core but a IR GHC uses after Core called STG. (Ive cleaned up the STG though so its not true syntax)
case = evaluation and ONLY place evaluation occurs (true in Core)let = allocation and ONLY place allocation occurs (not true in Core)letTo view STG use:
ghc -ddump-stg A.hs > A.stg
x + y, where x and y have type Int.
x & y must be represented by pointers to a possibly unevaluated objectx & y, add them, and box the resultThis can be a huge performance penalty in numeric heavy code if the implementation is naive
x will always be evaluated (i.e is 'strict') to avoid breaking the lazy semantics of HaskellConsider this factorial implementation in Haskell:
fac :: Int -> Int -> Int
fac a 0 = a
fac a n = fac (n*a) (n-1)STG
fac = \ a n -> case n of
I# n# -> case n# of
0# -> a
_ -> let one = I# 1;
x = n - one
y = n * a;
in fac y xfac will immediately evaluate the thunks and unbox the values!If we compile in GHC with optimisations turned on:
one = I# 0#
-- worker :: Int# -> Int# -> Int#
$wfac = \ a# n# -> case n# of
0# -> a#
n'# -> case (n'# -# 1#) of
m# -> case (n'# *# a#) of
x# -> $wfac x# m#
-- wrapper :: Int -> Int -> Int
fac = \ a n -> case a of
I# a# -> case n of
I# n# -> case ($wfac a# n#) of
r# -> I# r#fac is strict in both argumentsfac that uses unboxed types and no thunksfac though, referred to as the 'wrapper' to supply the correct type interface for other code.The idea of the SpecConstr pass is to extend the strictness and unboxing from before but to functions where arguments aren't strict in every code path.
Consider this Haskell function:
drop :: Int -> [a] -> [a]
drop n [] = []
drop 0 xs = xs
drop n (x:xs) = drop (n-1) xsn unboxed but it isn't strict in the first patternSo we get this code in STG:
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> xs
_ -> drop (I# (n# -# 1#)) ysn unboxedThe SpecConstr pass takes advantage of this to create a specialised version of drop that is only called after we have passed the first check where we may not want to evaluate n.
Basically we aren't specialising the whole function but a particular branch of it that is heavily used (ie. recursive)
drop n xs = case xs of
[] -> []
(y:ys) -> case n of
I# n# -> case n# of
0 -> xs
_ -> drop' (n# -# 1#) ys
-- works with unboxed n
drop' n# xs = case xs of
[] -> []
(y:ys) -> case n# of
0# -> xs
_ -> drop (n# -# 1#) ys-fspec-constr-threshol and -fspec-constr-count flagsFinal stage of GHC is compiling Core to an executable. The backend is in two parts:
Cmm is a low level imperative language used in GHC. Basically a very simple C like language. Just enough to abstract away hardware registers, call conventions:
So what has been handled and what is left to handle?
The way the operational semantics of the STG language is defined is by an abstract machine called 'The STG Machine'.
Lets just look at some of the details of the code generator. The final backends are all pretty straight forward (think simple C compiler). The important parts of the code generator are:
The STG machine represents function and data values as heap allocated closures. Delayed computations, thunks, are also represented by closure objects.
In GHC all Heap objects have the same layout:
| Closure | Info Table | ||
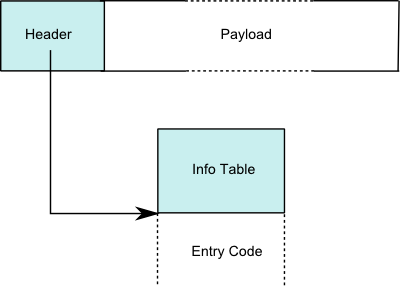
|

|
Data Constructors:
data G = G (Int -> Int) {-# UNPACK #-} !IntThunks:
range = between 1 10
f = \x -> let ys = take x range
in sum ysrange is a static thunk, ys is a dynamic thunk)Function Closures:
f = \x -> let g = \y -> x + y
in g xPartial Applications (PAP):
foldr (:)GHC has a very nice uniform way of managing the heap and stack.
id' x = xA_idzq_entry()
R1 = R2;
jump stg_ap_0_fast ();stg_ap_0_fast {
ENTER();
}
#define ENTER()
// ...
case
FUN,
// ...
PAP: { jump %ENTRY_CODE(Sp(0)); }
default: { info = %INFO_PTR(UNTAG(R1)); jump %ENTRY_CODE(info); }Calling a known Haskell function:
Haskell
x :: Int -> Int
x z = (+) 2 (id z)Cmm
I64[Hp - 8] = spH_info; // create thunk on heap
I64[Hp + 0] = R2; // R2 = z, store argument in closure
R2 = stg_INTLIKE_closure+289; // first argument (static closure for '2')
R3 = Hp - 16; // second argument (closure pointer)
jump base_GHCziBase_plusInt (); // call (+) functionWhat happens though when we are calling an unknown function?
Haskell
unknown_app :: (Int -> Int) -> Int -> Int
unknown_app f x = f xCmm
unknownzuapp_entry() {
cnO:
R1 = R2;
Sp = Sp + 4;
jump stg_ap_p_fast ();
}Here we don't call the function directly as we don't statically known the arity of the function.
To deal with this, the STG machine has several pre-compiled functions that handle 'generic application'
Haskell
10Cmm
section "data" {
A_ten_closure:
const ghczmprim_GHCziTypes_Izh_static_info;
const 10;
}I#)10)An optimization that GHC does is pointer tagging. The trick is to use the final bits of a pointer which are usually zero (last 2 for 32bit, 3 on 64) for storing a 'tag'.
One optimization tag bit enable is that we can detect if a closure has already been evaluated (by the presence of tag bits) and avoid entering it
Haskell
build_just :: a -> Maybe a
build_just x = Just xCmm
buildzujust_entry()
crp:
Hp = Hp + 16;
if (Hp > HpLim) goto crt; // Allocte heap space
I64[Hp - 8] = base_DataziMaybe_Just_con_info; // Just constructor tag
I64[Hp + 0] = R2; // store x in Just
R1 = Hp - 6; // setup R1 as argument to continuation
// (we do '- 6' and not '8' to set the pointer tag)
jump (I64[Sp + 0]) (); // jump to continuation
cru:
R1 = buildzujust_closure;
jump stg_gc_fun ();
crt:
HpAlloc = 16;
goto cru;
}Haskell
mycase :: Maybe Int -> Int
mycase x = case x of Just z -> z; Nothing -> 10Cmm
mycase_entry() // corresponds to forcing 'x'
crG:
R1 = R2; // R1 = 'x'
I64[Sp - 8] = src_info; // setup case continuation
Sp = Sp - 8;
if (R1 & 7 != 0) goto crL; // check pointer tag to see if x eval'd
jump I64[R1] (); // x not eval'd, so eval
crL:
jump src_info (); // jump to case continuation
}
src_ret() // case continuation
crC:
v::I64 = R1 & 7; // get tag bits of 'x' and put in local variable 'v'
if (_crD::I64 >= 2) goto crE; // can use tag bits to check which constructor we have
R1 = stg_INTLIKE_closure+417; // 'Nothing' case
Sp = Sp + 8; // pop stack
jump (I64[Sp + 0]) (); // jump to continuation ~= return
crE:
R1 = I64[R1 + 6]; // get 'z' thunk inside Just
Sp = Sp + 8; // pop stack
R1 = R1 & (-8); // clear tags on 'z'
jump I64[R1] (); // force 'z' thunk
}Lets take a look at the code for the (x + 1) thunk:
build_data :: Int -> Maybe Int
build_data x = Just (x + 1)Cmm
sus_entry()
cxa:
if (Sp - 24 < SpLim) goto cxc;
I64[Sp - 16] = stg_upd_frame_info; // setup update frame (closure type)
I64[Sp - 8] = R1; // set thunk to be updated (payload)
I64[Sp - 24] = sut_info; // setup continuation (+) continuation
Sp = Sp - 24; // increase stack
R1 = I64[R1 + 16]; // grab 'x' from environment
if (R1 & 7 != 0) goto cxd; // check if 'x' is eval'd
jump I64[R1] (); // not eval'd so eval
cxc: jump stg_gc_enter_1 ();
cxd: jump sut_info (); // 'x' eval'd so jump to (+) continuation
}
sut_ret()
cx0:
Hp = Hp + 16;
if (Hp > HpLim) goto cx5;
v::I64 = I64[R1 + 7] + 1; // perform ('x' + 1)
I64[Hp - 8] = ghczmprim_GHCziTypes_Izh_con_info; // setup Int closure
I64[Hp + 0] = v::I64; // setup Int closure
R1 = Hp - 7; // point R1 to computed thunk value (with tag)
Sp = Sp + 8; // pop stack
jump (I64[Sp + 0]) (); // jump to continuation ('stg_upd_frame_info')
cx6: jump stg_gc_enter_1 ();
cx5:
HpAlloc = 16;
goto cx6;
}(x + 1) it doesn't return to the continuation at the top of the stackI64[Sp - 16] = stg_upd_frame_info; // setup update frame (closure type)
I64[Sp - 8] = R1; // set thunk to be updated (payload)stg_upd_frame_info function

AMod_abc_entry:
entry:
_v = R2 // collect arguments
_w = R3
if (Sp - 40 < SpLim) goto spL // check enough stack free
Hp = Hp + 20 // allocate heap space
if (Hp > HpLim) goto hpL // check allocation is ok
[... funtion code now we have stack and heap space needed ...]
Sp = Sp - 32 // bump stack pointer to next free word
jump ... // jump to next continuation
hpL:
HpAlloc = 20 // inform how much hp space we need
spL:
R1 = AMod_abc_closure; // set return point
jump stg_gc_fun // call GCHp and Sp registers for allocation after we check there is enough space.No lecture on Compilers is complete without assembly code!
add :: Int -> Int -> Int
add x y = x + y + 2A_add_info:
.LcvZ:
leaq -16(%rbp),%rax
cmpq %r15,%rax
jb .Lcw1
movq %rsi,-8(%rbp)
movq %r14,%rbx
movq $sul_info,-16(%rbp)
addq $-16,%rbp
testq $7,%rbx
jne sul_info
jmp *(%rbx)
.Lcw1:
movl $A_add_closure,%ebx
jmp *-8(%r13)
sul_info:
.LcvS:
movq 8(%rbp),%rax
movq 7(%rbx),%rcx
movq %rcx,8(%rbp)
movq %rax,%rbx
movq $suk_info,0(%rbp)
testq $7,%rbx
jne suk_info
jmp *(%rbx)
suk_info:
.LcvK:
addq $16,%r12
cmpq 144(%r13),%r12
ja .LcvP
movq 7(%rbx),%rax
addq $2,%rax
movq 8(%rbp),%rcx
addq %rax,%rcx
movq $ghczmprim_GHCziTypes_Izh_con_info,-8(%r12)
movq %rcx,0(%r12)
leaq -7(%r12),%rbx
addq $16,%rbp
jmp *0(%rbp)
.LcvP:
movq $16,184(%r13)
.LcvQ:
jmp *-16(%r13)
So that's is all I can cover in this lecture.
Here are some resources to learn about GHC, they were also used to create these slides:
Here are some resources to learn about GHC, they were also used to create these slides:
Here are some resources to learn about GHC, they were also used to create these slides: